Table of Contents

1. 集成学习

1. 集成学习

顾名思义，集成学习（ensemble learning）指的是将多个学习器进行有效地结合，组建一个“学习器委员会”，其中每个学习器担任委员会成员并行使投票表决权，使得委员会最后的决定更能够四方造福普度众生~...~，即其泛化性能要能优于其中任何一个学习器。

集成学习（ensemble learning）通过构建并结合多个学习期来完成学习任务，有时也被称为多分类器系统（multi-classifier system）、基于委员会的学习（committee-based learning）等。

这一章的内容大致如下：

个体与集成：同质集成和异质集成有什么不同？集成学习对个体学习器有什么要求？集成学习研究的核心是什么？集成学习分哪两大类？
Boosting：Boosting的基本概念？AdaBoost算法的流程？如何基于加性模型最小化指数损失函数来推导？怎样处理基学习算法无法处理带权样本的情况？Boosting的优势是什么？
Bagging与随机森林：Bagging算法如何获得各个基学习器的训练集？预测时如何进行结合？相比AdaBoost有什么优势？随机森林的核心思想是什么？相比Bagging有什么优势？
结合策略：结合多个学习器有什么好处？平均法是怎样的？投票法是怎样的？学习法又是怎样的？
多样性：如何进行误差-分歧分解？说明了什么？有哪些多样性度量指标？有哪些增强多样性的手段？

1.1. 个体与集成

集成学习先产生一组个体学习器（individual learner），再用某种策略将它们结合起来。

当所有个体学习器都由同样的学习算法生成时，也即集成中只包含同种类型的个体学习器时，称为同质（homogeneous）集成，这些个体学习器又被称为基学习器（base learner），相应的学习算法称为基学习算法（base learning algorithm）；

当个体学习器由不同的学习算法生成时，称为异质（heterogenous）集成，这些个体学习器称为组件学习器（component learner）或直接称为个体学习器。

集成学习通过结合多个学习器，通常能获得比单一学习器更优越的泛化性能，对弱学习器（weak learner）的提升尤为明显。注：弱学习器即略优于随机猜测的学习器，例如二分类任务中精度略高于50%。虽然理论上，集成弱学习器已经能获得很好的性能。但现实任务中，人们往往会使用比较强的学习器。

当我们使用集成学习的时候，我们其实是希望不同的个体学习器产生互补的效果，使得某个学习器错误的地方能有机会被其他学习器纠正过来，这就要求个体学习器应该尽量“不同”，即具有多样性；同时我们希望这种互补不会把正确改为错误，这就要求个体学习器应该尽量“准确”。合起来就是集成学习研究的核心——如何产生并结合“好而不同”的个体学习器。

根据个体学习器的生成方式，集成学习方法大致可分为两个大类：

个体学习器间存在强依赖关系，必须串行生成的序列化方法，例如：Boosting算法族；
个体学习器间不存在强依赖关系，可同时生成的并行化方法，例如：Bagging，随机森林；

上篇主要介绍了鼎鼎大名的EM算法，从算法思想到数学公式推导（边际似然引入隐变量，Jensen不等式简化求导），EM算法实际上可以理解为一种坐标下降法，首先固定一个变量，接着求另外变量的最优解，通过其优美的“两步走”策略能较好地估计隐变量的值。本篇将继续讨论下一类经典算法--集成学习。

集成学习的基本结构为：先产生一组个体学习器，再使用某种策略将它们结合在一起。集成模型如下图所示：

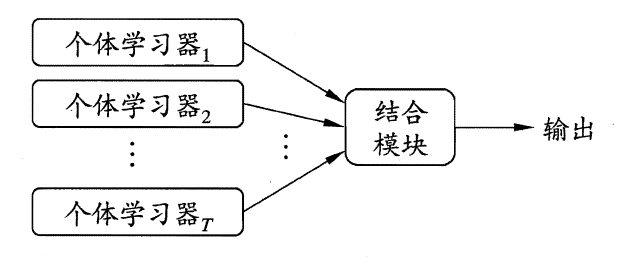
在上图的集成模型中，若个体学习器都属于同一类别，例如都是决策树或都是神经网络，则称该集成为同质的（homogeneous）;若个体学习器包含多种类型的学习算法，例如既有决策树又有神经网络，则称该集成为异质的（heterogenous）。

同质集成：个体学习器称为“基学习器”（base learner），对应的学习算法为“基学习算法”（base learning algorithm）。
异质集成：个体学习器称为“组件学习器”（component learner）或直称为“个体学习器”。

上面我们已经提到要让集成起来的泛化性能比单个学习器都要好，虽说团结力量大但也有木桶短板理论调皮捣蛋，那如何做到呢？这就引出了集成学习的两个重要概念：准确性和多样性（diversity）。准确性指的是个体学习器不能太差，要有一定的准确度；多样性则是个体学习器之间的输出要具有差异性。通过下面的这三个例子可以很容易看出这一点，准确度较高，差异度也较高，可以较好地提升集成性能。

现在考虑二分类的简单情形，假设基分类器之间相互独立（能提供较高的差异度），且错误率相等为 ε，则可以将集成器的预测看做一个伯努利实验，易知当所有基分类器中不足一半预测正确的情况下，集成器预测错误，所以集成器的错误率可以计算为：

此时，集成器错误率随着基分类器的个数的增加呈指数下降，但前提是基分类器之间相互独立，在实际情形中显然是不可能的，假设训练有A和B两个分类器，对于某个测试样本，显然满足：P（A=1 | B=1）> P（A=1），因为A和B为了解决相同的问题而训练，因此在预测新样本时存在着很大的联系。因此，个体学习器的“准确性”和“差异性”本身就是一对矛盾的变量，准确性高意味着牺牲多样性，所以产生“好而不同”的个体学习器正是集成学习研究的核心。现阶段有三种主流的集成学习方法：Boosting、Bagging以及随机森林（Random Forest），接下来将进行逐一介绍。

1.2. Boosting

Boosting是一种串行的工作机制，即个体学习器的训练存在依赖关系，必须一步一步序列化进行。其基本思想是：增加前一个基学习器在训练训练过程中预测错误样本的权重，使得后续基学习器更加关注这些打标错误的训练样本，尽可能纠正这些错误，一直向下串行直至产生需要的T个基学习器，Boosting最终对这T个学习器进行加权结合，产生学习器委员会。

Boosting族算法最著名、使用最为广泛的就是AdaBoost，因此下面主要是对AdaBoost算法进行介绍。AdaBoost使用的是指数损失函数，因此AdaBoost的权值与样本分布的更新都是围绕着最小化指数损失函数进行的。看到这里回想一下之前的机器学习算法，不难发现机器学习的大部分带参模型只是改变了最优化目标中的损失函数：如果是Square loss，那就是最小二乘了；如果是Hinge Loss，那就是著名的SVM了；如果是log-Loss，那就是Logistic Regression了。

1.2.1. AdaBoost

定义基学习器的集成为加权结合，则有：

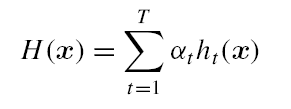
AdaBoost算法的指数损失函数定义为：

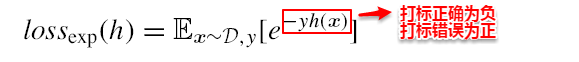
具体说来，整个Adaboost 迭代算法分为3步：

初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。
训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。

整个AdaBoost的算法流程如下所示：

可以看出：AdaBoost的核心步骤就是计算基学习器权重和样本权重分布，那为何是上述的计算公式呢？这就涉及到了我们之前为什么说大部分带参机器学习算法只是改变了损失函数，就是因为大部分模型的参数都是通过最优化损失函数（可能还加个规则项）而计算（梯度下降，坐标下降等）得到，这里正是通过最优化指数损失函数从而得到这两个参数的计算公式，具体的推导过程此处不进行展开。

Boosting算法要求基学习器能对特定分布的数据进行学习，即每次都更新样本分布权重，这里书上提到了两种方法：“重赋权法”（re-weighting）和“重采样法”（re-sampling），书上的解释有些晦涩，这里进行展开一下：

重赋权法 : 对每个样本附加一个权重，这时涉及到样本属性与标签的计算，都需要乘上一个权值。
重采样法 : 对于一些无法接受带权样本的及学习算法，适合用“重采样法”进行处理。方法大致过程是，根据各个样本的权重，对训练数据进行重采样，初始时样本权重一样，每个样本被采样到的概率一致，每次从N个原始的训练样本中按照权重有放回采样N个样本作为训练集，然后计算训练集错误率，然后调整权重，重复采样，集成多个基学习器。

从偏差-方差分解来看：Boosting算法主要关注于降低偏差，每轮的迭代都关注于训练过程中预测错误的样本，将弱学习提升为强学习器。从AdaBoost的算法流程来看，标准的AdaBoost只适用于二分类问题。在此，当选为数据挖掘十大算法之一的AdaBoost介绍到这里，能够当选正是说明这个算法十分婀娜多姿，背后的数学证明和推导充分证明了这一点，限于篇幅不再继续展开。

1.2.2. Gradient Boosting 梯度提升

1.3. Bagging

相比之下，Bagging与随机森林算法就简洁了许多，上面已经提到产生“好而不同”的个体学习器是集成学习研究的核心，即在保证基学习器准确性的同时增加基学习器之间的多样性。而这两种算法的基本思（tao）想（lu）都是通过“自助采样”的方法来增加多样性。

Bagging是一种并行式的集成学习方法，即基学习器的训练之间没有前后顺序可以同时进行，Bagging使用“有放回”采样的方式选取训练集，对于包含m个样本的训练集，进行m次有放回的随机采样操作，从而得到m个样本的采样集，这样训练集中有接近36.8%的样本没有被采到。按照相同的方式重复进行，我们就可以采集到T个包含m个样本的数据集，从而训练出T个基学习器，最终对这T个基学习器的输出进行结合。

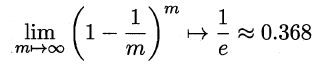
Bagging算法的流程如下所示：

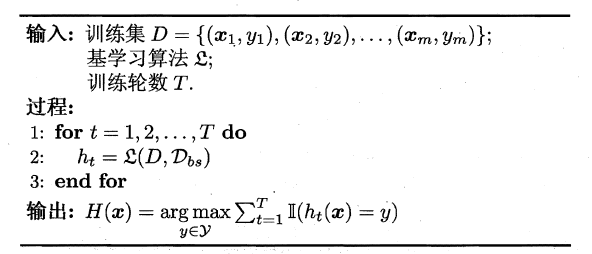
可以看出Bagging主要通过样本的扰动来增加基学习器之间的多样性，因此Bagging的基学习器应为那些对训练集十分敏感的不稳定学习算法，例如：神经网络与决策树等。从偏差-方差分解来看，Bagging算法主要关注于降低方差，即通过多次重复训练提高稳定性。不同于AdaBoost的是，Bagging可以十分简单地移植到多分类、回归等问题。总的说起来则是：AdaBoost关注于降低偏差，而Bagging关注于降低方差。

1.3.1. 随机森林

随机森林（Random Forest）是Bagging的一个拓展体，它的基学习器固定为决策树，多棵树也就组成了森林，而“随机”则在于选择划分属性的随机，随机森林在训练基学习器时，也采用有放回采样的方式添加样本扰动，同时它还引入了一种属性扰动，即在基决策树的训练过程中，在选择划分属性时，RF先从候选属性集中随机挑选出一个包含K个属性的子集，再从这个子集中选择最优划分属性，一般推荐K=log2（d）。

这样随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动，从而进一步提升了基学习器之间的差异度。

相比决策树的Bagging集成，随机森林的起始性能较差（由于属性扰动，基决策树的准确度有所下降），但随着基学习器数目的增多，随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划分属性，随机森林只在属性集的一个子集中选择划分属性，因此训练效率更高。

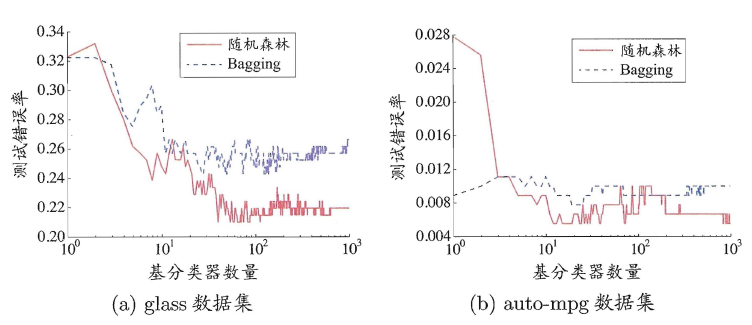
随机森林分类

sklearn.ensemble.RandomForestClassifier(n_estimators=100, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None)

参数详解

n_estimators[defaults=100]
也就是弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，计算量会太大，并且n_estimators到一定的数量后，再增大n_estimators获得的模型提升会很小，所以一般选择一个适中的数值。默认是100。
criterion
即CART树做划分时对特征的评价标准。分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini,另一个可选择的标准是信息增益。回归RF对应的CART回归树默认是均方差mse，另一个可以选择的标准是绝对值差mae。一般来说选择默认的标准就已经很好的。
max_depth[defaults=Nnone]
- 决策树最大深度 max_depth: 默认可以不输入，如果不输入的话，决策树在建立子树的时候不会限制子树的深度。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
min_samples_split
- 内部节点再划分所需最小样本数min_samples_split: 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
min_samples_leaf
叶子节点最少样本数 。min_samples_leaf: 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
min_weight_fraction_leaf
- 叶子节点最小的样本权重：这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
max_features[defaults=auto]
可以填 int, float, string or None, optional
随机森林划分时，考虑到的最大特征数量。max_features
If auto, then max_features=sqrt(n_features).
If sqrt, then max_features=sqrt(n_features) (same as “auto”).
If log2, then max_features=log2(n_features).
If None, then max_features=n_features.
如果是整数，代表考虑的特征绝对数。
如果是浮点数，代表考虑特征百分比，即考虑（百分比xN）取整后的特征数。其中N为样本总特征数。
max_leaf_nodes[defaults=None]
最大叶子节点数max_leaf_nodes: 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，。
min_impurity_decrease
python if impurity(n)-impurity(n+1)< min_impurity_decrease: break make_new_tree
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.

The weighted impurity decrease equation is the following:

N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
where N is the total number of samples, N_t is the number of samples at the current node, N_t_L is the number of samples in the left child, and N_t_R is the number of samples in the right child.

N, N_t, N_t_R and N_t_L all refer to the weighted sum, if sample_weight is passed.

New in version 0.19.
min_impurity_split
- 节点划分最小不纯度 min_impurity_split: 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数、均方差、商增益)小于这个阈值，则该节点不再生成子节点。即为叶子节点。一般不推荐改动默认值1e-7。
if impurity< min_impurity_split: break make_new_tree
bootstrap : boolean, optional (default=True)
- 在构建每颗树的时候，是否采用bootstrap采样。[True] bootstrap 采样，[False] ，全部数据都用用户构建。
oob_score
- oob_score :即是否采用袋外样本来评估模型的好坏。默认识False。个人推荐设置为True，因为袋外分数反应了一个模型拟合后的泛化能力。

随机森林回归

class sklearn.ensemble.RandomForestRegressor(n_estimators=’warn’, criterion=’mse’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False)

重要参数
1. criterion : string, optional (default=”mse”)
The function to measure the quality of a split. Supported criteria are “mse” for the mean squared error, which is equal to variance reduction as feature selection criterion, and “mae” for the mean absolute error.

New in version 0.18: Mean Absolute Error (MAE) criterion

1.4. 结合策略

结合策略指的是在训练好基学习器后，如何将这些基学习器的输出结合起来产生集成模型的最终输出，下面将介绍一些常用的结合策略：

1.4.1. 平均法（回归问题）

1.4.1.1. 简单平均

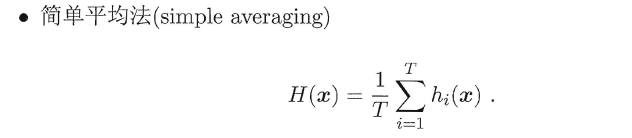
1.4.1.2. 加权平均

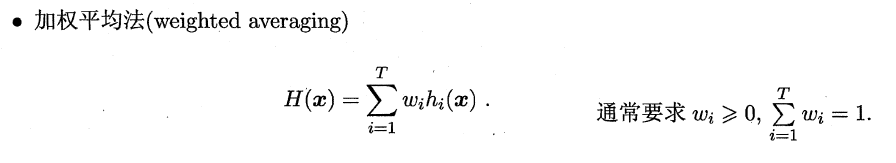
易知简单平均法是加权平均法的一种特例，加权平均法可以认为是集成学习研究的基本出发点。由于各个基学习器的权值在训练中得出，一般而言，在个体学习器性能相差较大时宜使用加权平均法，在个体学习器性能相差较小时宜使用简单平均法。

1.4.2. 投票法（分类问题）

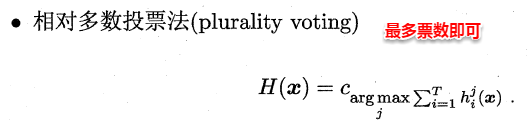
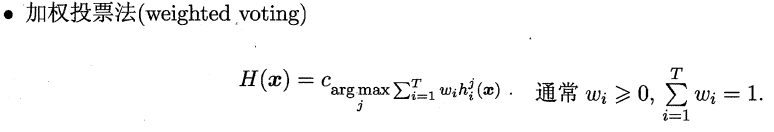
绝对多数投票法（majority voting）提供了拒绝选项，这在可靠性要求很高的学习任务中是一个很好的机制。同时，对于分类任务，各个基学习器的输出值有两种类型，分别为类标记和类概率。

一些在产生类别标记的同时也生成置信度的学习器，置信度可转化为类概率使用，一般基于类概率进行结合往往比基于类标记进行结合的效果更好，需要注意的是对于异质集成，其类概率不能直接进行比较，此时需要将类概率转化为类标记输出，然后再投票。

1.4.3. 学习法

不使用简单的函数（如硬投票、平均）来聚合集合中所有分类器的预测，我们为什么不训练一个模型来执行这个聚合？学习法是一种更高级的结合策略，即学习出一种“投票”的学习器，

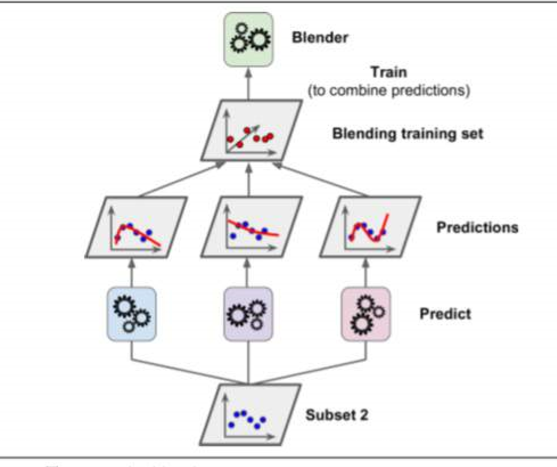
1.4.3.1. Stacking

Stacking 是stacked generalization的简称。
Stacking 是学习法的典型代表。Stacking的基本思想是：首先训练出T个基学习器，对于一个样本它们会产生T个输出，将这T个基学习器的输出与该样本的真实标记作为新的样本，m个样本就会产生一个m*T的样本集，来训练一个新的“投票”学习器。投票学习器的输入属性与学习算法对Stacking集成的泛化性能有很大的影响，书中已经提到：投票学习器采用类概率作为输入属性，选用多响应线性回归（MLR）一般会产生较好的效果。

meta-learner 的选择

Generally Ensemble Learners like Random Forests,XGBoost,GradientBoost etc are used as meta learner.But any algorithm can be used as a meta learner there is no rule that we have to use only ensemble learners.

1.5. 多样性（diversity）

在集成学习中，基学习器之间的多样性是影响集成器泛化性能的重要因素。因此增加多样性对于集成学习研究十分重要，一般的思路是在学习过程中引入随机性，常见的做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。

数据样本扰动，即利用具有差异的数据集来训练不同的基学习器。例如：有放回自助采样法，但此类做法只对那些不稳定学习算法十分有效，例如：决策树和神经网络等，训练集的稍微改变能导致学习器的显著变动。
输入属性扰动，即随机选取原空间的一个子空间来训练基学习器。例如：随机森林，从初始属性集中抽取子集，再基于每个子集来训练基学习器。但若训练集只包含少量属性，则不宜使用属性扰动。
输出表示扰动，此类做法可对训练样本的类标稍作变动，或对基学习器的输出进行转化。
算法参数扰动，通过随机设置不同的参数，例如：神经网络中，随机初始化权重与随机设置隐含层节点数。

在此，集成学习就介绍完毕，看到这里，大家也会发现集成学习实质上是一种通用框架，可以使用任何一种基学习器，从而改进单个学习器的泛化性能。据说数据挖掘竞赛KDDCup历年的冠军几乎都使用了集成学习，看来的确是个好东西~

1.6. Q&A

问：假设抛硬币正面朝上的概率为 $p$，反面朝上的概率为 $1-p$。令 $H(n)$ 代表抛 $n$ 次硬币所得正面朝上的次数，则最多 $k$ 次正面朝上的概率为

$$P(H(n) \leq k) = \sum_{i=0}^k \binom{n}{i} p^i (1-p)^{n-i}$$

对 $\delta > 0,\quad k=(p-\delta)n$，有 Hoeffding 不等式

$$P(H(n) \leq (p-\delta)n) \leq e^{-2\delta^2n}$$

试推导出式（8.3）

问：对于 0/1 损失函数来说，指数损失函数并非仅有的一直替代函数，考虑式（8.5），试证明：任意损失函数 $\ell(-f(\mathbf{x}H(\mathbf{x})))$，若对于 $H(\mathbf{x})$ 在区间 $-\inf,\delta$ 上单调递减，则 $\ell$ 是 0/1 损失函数的一致替代函数。

问：从网上下载或自己编程实现 Adaboost，以不剪枝决策树为基学习器，在西瓜数据集 3.0$\alpha$ 上训练一个 AdaBoost 集成，并与图8.4进行比较。

问：GradientBoosting 是一种常用的 Boosting 算法，试析其与 AdaBoost 的异同。

问：试编程实现 Bagging，以决策树桩为基学习器，在西瓜数据集 3.0$\alpha$ 上训练一个 Bagging 集成，并与图8.6进行比较。

问：试析 Bagging 通常为何难以提升朴素贝叶斯分类器的性能。

问：试析随即森林为何比决策树 Bagging 集成的训练速度更快。

问：MultiBoosting 算法将 AdaBoost 作为 Bagging 的基学习器，Iterative Bagging 算法则是将 Bagging 作为 AdaBoost 的基学习器，试比较二者的优缺点。

问：试设计一种可视的多样性度量，对习题8.3和习题8.5中得到的集成进行评估，并与 $\kappa$-误差图比较。

问：试设计一种能提升 $k$ 近邻分类器性能的集成学习算法。