清华大学-数据挖掘课程笔记
[TOC]
1. 走进数据科学:博大精深,美不胜收
1.1 走进数据科学(基本概念)
接下来给出一些基本概念的定义:
示例(instance),样本(sample)
数据集中的每条记录是对一个事件或对象(比如这里的西瓜)的描述,也称作示例或者样本。特别地,有时会把整个数据集称为一个样本,因为数据集可以看作是从样本空间中抽样所得。这时候就需要根据上下文信息来进行判断了。
属性(attribute),特征(feature),属性值(attribute value)
对象具备一些性质,并由此可以进行区分,这些性质就称为属性或者特征,比方说表格中的色泽、根蒂和敲声。不同对象在这些属性上会有不同的取值,这个取值就称为属性值。
属性空间(attribute space),样本空间(sample space),输入空间,特征向量(feature vector)
由属性张成的空间,比方说上面的表格中有3个属性,那就可以张成一个3维空间,每个样本都可以用空间中的一个点来表示,这个点对应于一个坐标向量,所以有时也把一个样本称为一个特征向量。
维数(dimensionality)
即数据集中每个样本拥有的特征数目。
学习(learning),训练(training),训练样本(training sample),训练示例(training instance)
从数据中获的模型的过程。在这个过程中使用的数据称为训练数据,里面的每个样本称为一个训练样本,也称训练示例或训练例。训练样本的集合就是训练集。
模型(model),学习器(learner),假设(hypothesis),真相(ground-truth)
模型有时也称为学习器,可以看作一组参数的有序集合,能够把属性空间映射到输出空间上。每一个模型对应于一个假设,也即数据存在的某种规律。真相指的是真正存在的规律,学习就是为了接近真相。
如果我们希望通过机器学习来实现预测(prediction),那么只有样本是不够的,要让机器明白怎样的样本会产生怎样的结果,还需要为每个样本设置标记,标记有可能是离散值(分类任务),也可能是连续值(回归任务)。带标记的数据集如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 标记 |
|---|---|---|---|---|
| 001 | 青绿 | 蜷缩 | 浊响 | 好瓜 |
| 002 | 乌黑 | 稍蜷 | 沉闷 | 坏瓜 |
| 003 | 浅白 | 硬挺 | 清脆 | 坏瓜 |
标记(label),样例(example),标记空间(label space),输出空间
标记指示的是对象的类别或者事件的结果,样本和标记组合起来就是样例。所有标记的集合称为标记空间,也称为输出空间。
分类(classification),回归(regression),聚类(clustering)
根据预测值的不同,可以把任务分为几种不同的类别。若预测的是离散值,比如“好瓜”,“坏瓜”,则该任务称为分类任务;若预测的是连续值,比如瓜的重量,则该任务称为回归任务;还有一种聚类任务,旨在基于某种度量将样本分为若干个簇(cluster),使得同一簇内尽量相似,不同簇间尽量相异。聚类任务不需要对样本进行标记。
特别地,只涉及两种类别的分类任务称为二分类任务(binary classification),通常称一个类为正类(positive class),另一个类为反类或者负类(negative class)。涉及到多个类别的分类任务就称为多分类(multi-class classification)任务。
测试(testing),测试样本(testing sample),测试示例(testing instance)
训练完成后,使用模型预测新样本的标记这个过程称为测试。测试中使用到的样本称为测试样本,也称测试示例或测试例。
监督学习(supervised learning),无监督学习(unsupervised learning)
根据训练样本是否标记可以把任务分为两大类,需要标记的是监督学习,不需要标记的是无监督学习。前者的代表是回归和分类,后者的代表是聚类。
泛化(generalization)能力
让机器进行学习的目标并不仅仅是为了让模型能在训练数据上有好的表现,我们更希望模型在新的样本上也能有良好的表现。模型适用于新样本的能力就称为泛化能力,泛化能力好的模型能够更好地适用于整个样本空间。
独立同分布(independent and identically distributed)
一般来说,训练数据只占训练空间很少的一部分,当我们希望这一小部分的采样能够很好地反映整个样本空间的情况,从而令学得的模型具有良好的泛化能力。通常假设样本空间中的所有样本都服从于一个未知的分布(distribution),并且训练样本都是从该分布上独立采样所得,这就称为独立同分布。训练样本越多,越能反映该分布的特性,从而能学得泛化能力更强的模型。
1.2 整装待发
1.3 学而不思则罔
学习方法/资料 行业背景
1.4 知行合一
1.5 从数据到知识
1.5 模型 比较检验
1.4.1 假设检验
1.4.2 交叉验证t检验
1.4.3 McNemar检验
1.4.4 Friedman检验与Nemenyi后续检验
1.6 分类问题
1.6.1 类型
1.6.1.1 二分类
0-1 问题
1.6.1.2 多分类
1.6.2 评价
1.6.2.1 评价方法
测试集(testing set):用来测试学习器对新样本的判别能力
测试误差(testing error):在测试集上的误差,泛化误差的近似
Note: 测试集应该尽量和训练集互斥
所以需要对给定的数据集进行适当的处理,产出训练集S和测试集T
1.6.2.2.1 留出法
D=[1,2,3,4,5,6,7,8,9,10] Train=[1,2,3,4,5,6,7,8] Test=[9,10]
留出法(hold-out)直接将数据集划分为两个互斥的集合。另个集合交集为空,并集为整个集合。
但是需要注意,训练集和测试集的划分要尽可能保持数据分布的一致性。
保留类别比例的采样方式通常称为“分层采样”(stratified sampling)。
单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分、重复进行试验评估后取平均值作为留出法的评估结果。
1.6.2.2.2 交叉验证法
又称为k折交叉验证(k-fold cross validation)
D=[1,2,3,4,5,6] train=[3,4,5,6|1,2,5,6,|1,2,3,4] val=[1,2,|3,4,|5,6]
-
留一法
特别地,令k=数据集样本数的交叉验证称为留一法(Leave-One-Out,简称LOO),即有多少样本就进行多少次训练/验证,并且每次只留下一个样本做验证。这样做的好处是不需要担心随即样本划分带来的误差,因为这样的划分是唯一的。一般来说,留一法的评估结果被认为是比较准确的。但是!当数据集较大时,使用留一法需要训练的模型太多了!这种计算开销是难以忍受的!
D=[1,2,3,4,5]
train=[2,3,4,5,|1,3,4,5,|1,2,4,5,|1,2,3,5,|1,2,3,4]
val=[1,|2,|3,|4,|5]
1.6.2.2.3 自助法(bootstrapping,有放回采样)
| 留出法和交叉验证法 | 需要对数据集进行划分,使得训练所用的数据集比源数据集小,引入了一些因规模不同而造成的偏差 |
| ? | 避免规模不同造成的影响 |
自助法(bootstrapping) 正是我们需要的答案,以 自助采样(bootstrap sampling) 为基础,对包含m个样本的源数据集进行有放回的m次采样以获得同等规模的训练集。在这m次采样中都不被抽到的概率大约为0.368,
也即源数据集中有大约1/3的样本是训练集中没有的。因此,我们可以采用这部分样本作为验证集,所得的结果称为 包外估计(out-of-bag estimate)。
优势:
适用于:数据集小,难以划分训练/测试集
可从原始数据集中衍生出多个不同的数据集,对集成学习有好处
不足:
* 改变了原始数据集的分布,引入估计偏差 ,若数据量足够 不需要生成。
1.6.2.2 评价指标
一般性
| 指标 | 描述 |
| --------------------------------------------------------: | -------------------------------------------------: |
| 错误率(error rate): | 分类错误的样本数占样本总数的比例 |
| 精度(accuracy): | 精度 = 1 - 错误率 |
| 误差(error): | 学习器的预测输出与样本真实输出之间的差异 |
| 训练误差(training error)或经验误差(empirical error): | 学习器在训练集上的误差 |
| 泛化误差(generalization error): | 学习器在新样本上的误差。 |
| 过拟合(overfitting): | 把训练样本自身的特点当成普遍特点,导致泛化能力下降 |
| 欠拟合(underfitting): | 对训练样本的一般性质尚未学好 |
2.3.1 错误率与精度
二分类问题
| 真实情况 | 预测结果 | |
|---|---|---|
| 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
| 指标(中) | 指标(EN) | 计算 | 含义 |
|---|---|---|---|
| 精度 | accuracy | $$accuracy = \frac | 整体数据中猜对了多少 |
| 查准率,准确率 | precision | $$precision = \frac | 避免错误的能力,分母是模型预测的正例数目 |
| 查全率,召回率,真正例率 | recall | $$recall = \frac | 用于衡量模型 避免缺漏 的能力,分母是测试样本真正包含的正例数目。 |
| F1 | F1 | $$\frac | 是查准率和查全率的调和平均,用于综合考虑这两个性能度量。 |
| $F_\beta$ | $F_\beta$ | $$\frac | $\beta>0$度量了查全率对查准率的相对重要性,等于1时$F_\beta$ 退化为F1,小于1时查准率更重要,大于1时查全率更重要 |
| 查全率,召回率,真正例率 | TPR,True Positive Rate | $$TPR = \frac | 用于衡量模型 避免缺漏 的能力,分母是测试样本真正包含的正例数目 |
| 假正例率 | FPR,False Positive Rate) | $$FPR = \frac | 用于衡量模型 存在缺漏 的能力,分母是测试样本真正包含的正例数目 |
| 受试者工作特征 | ROC,Receiver Operating Characteristic | $$ y=TPR = \frac | |
| ROC曲线下的面积 | AUC(Area Under ROC Curve) | $$AUC=\frac | 越大越好 |
| 排序损失 | loss | $$AUC = 1 - \ell_ | 越小越好 |
TPR其实就等于召回率。在绘制ROC曲线时,纵轴为TPR,横轴为FPR。首先按预测值对样本进行排序,然后按序逐个把样本预测为正例,并计算此时的TPR和FPR,然后在图上画出该点,并与前一个点连线。如下图:
有两个值得注意的特例:
-
经过 (0,1) 点的曲线,这代表所有正例都在反例之前出现(否则会先出现假正例从而无法经过 (0,1) 点),这是一个理想模型,我们可以设置一个阈值,完美地分割开正例和反例。
-
对角线,这对应于随机猜测模型,可以理解为真正例和假正例轮换出现,即每预测对一次接下来就预测错一次,可以看作是随机猜测的结果。
2.3.4 代价敏感错误率与代价曲线
1.6.3 分类方法
- knn
- 朴树贝叶斯
- svm
- 决策树
- 逻辑回归
1.7 聚类及其它数据挖掘问题
无监督问题
1.8 隐私保护与并行计算
1.8.1 隐私保护
1.8.2 并行计算
1.9 迷雾重重
盲人摸象
1.9.1 比较检验
看起来似乎有了获取测试集$^{*}$的评估方法和用于比较模型的性能度量之后,就能够通过不同模型在测试集上的性能表现来判断优劣了。但是!事实上,在机器学习中,模型比较并不是这样简单的比大小,而是要考虑更多。
注:指验证集,但无论是书中还是论文中,都使用测试集较多,明白两者的区别就可以了。
在模型比较中,主要有以下三个重要考虑:
- 测试集上的性能只是泛化性能的近似,未必相同;
- 测试集的选择对测试性能有很大影响,即使规模一致,但测试样例不同,结果也不同;
- 一些机器学习算法有随机性,即便算法参数相同,在同一测试集上跑多次,结果也可能不同;
那么应该如何有效地进行模型比较呢?答案是采用假设检验(hypothesis test)。基于假设检验的结果,我们可以推断出,若在测试集上观察到模型A优于B,则是否A的泛化性能在统计意义上也优于B,以及做这个结论的把握有多大。
本小节首先介绍最基本的二项检验和t检验,然后再深入介绍其他几种比较检验方法。默认以错误率作为性能度量。
几个基础概念:
- 置信度:表示有多大的把握认为假设是正确的。
- 显著度:也称“显著性水平”,表示假设出错的概率。显著度越大,假设被拒绝的可能性越大。
- 自由度:不被限制的样本数,也可以理解为能自由取值的样本数,记为 $v$ 或 $df$。
1.9.1 单个模型、单个数据集上的泛化性能检验
我们有多大把握相信对一个模型泛化性能的假设?
# 1.9.1.1 二项检验
在进行比较检验前,完成了一次模型预测,已知测试错误率为 $\hat{\epsilon}$。
一个泛化错误率为 $\epsilon$ 的模型在 $m$ 个样本上预测错 $m'$ 个样本的概率为:
$$ P(\hat{\epsilon};\epsilon) = \binom{m}{m'} \epsilon^{m'} (1-\epsilon)^{m - m'}$$
这个概率符合二项分布:

又因为已知测试错误率为 $\hat{\epsilon}$,也即知道了该模型在 $m$ 个样本上实际预测错 了$\hat{\epsilon} \times m$ 个样本。代入公式,对 $\epsilon$ 求偏导会发现,给定这些条件时,$\epsilon = \hat{\epsilon}$ 的概率是最大的。
使用二项检验(binomial test),假设泛化错误率 $\epsilon \leq \epsilon_0$,并且设定置信度为 $1-\alpha$。则可以这样定义错误率的阈值 $\overline{\epsilon}$:
$$\overline{\epsilon} = \max{\epsilon} \qquad s.t. \qquad \sum_{i=\epsilon_0 \times m+1}^m \binom{m}{i}\epsilon^i (1-\epsilon)^{m-i} < \alpha$$
其中 $s.t.$ 表示左式在右边条件满足时成立。右式计算的是发生不符合假设的事件的总概率,如果我们要有 $1-\alpha$ 的把握认为假设成立,那么发生不符合假设的事件的总概率就必须低过 $\alpha$。
在满足右式的所有 $\epsilon$ 中,选择最大的作为阈值 $\overline{\epsilon}$。如果在测试集中观测到的测试错误率 $\hat{\epsilon}$ 是小于阈值 $\overline{\epsilon}$的, 我们就能以$1-\alpha$ 的把握认为假设成立,即该模型的泛化误差 $\epsilon \leq \epsilon_0$。
# 1.9.1.2 t检验
二项检验只用于检验某一次测试的性能度量,但实际任务中我们会进行多次的训练/测试,得到多个测试错误率,比方说进行了k次测试,得到 $\hat{\epsilon}_1$,$\hat{\epsilon}_2$, ... ,$\hat{\epsilon}_k$。这次就会用到t检验(t-test)。
定义这 $k$ 次测试的平均错误率 $\mu$ 和方差 $\sigma^2$:
$$\mu = \frac{1}{k} \sum_{i=1}^k \hat{\epsilon_i}$$
$$\sigma^2 = \frac{1}{k-1} \sum_{i=1}^k (\hat{\epsilon_i} - \mu)^2$$
注意!这里使用的是无偏估计的样本方差,分母是 $k-1$,因为当均值确定,并且已知 $k-1$ 个样本的值时,第 $k$ 个样本的值是可以算出来的,也可以说是受限的。
假设泛化错误率 $\epsilon = \epsilon_0$,并且设定显著度为 $\alpha$。计算统计量t:
$$t = \frac{\sqrt{k}(\mu-\epsilon_0)}{\sigma}$$
该统计量服从自由度 $v = k-1$ 的t分布,如下图:

自由度越大,约接近于正态分布,自由度为无穷大时变为标准正态分布($\mu=0$,$\sigma=1$)。
如果计算出的t统计量落在临界值范围 [$t_{-a/2}$,$t_{a/2}$] 之内(注:临界值由自由度 $k$ 和显著度 $\alpha$ 决定,通过查表得出),我们就能以$1-\alpha$ 的把握认为假设成立,即该模型的泛化误差 $\epsilon = \epsilon_0$。
1.9.2 两个模型/算法、单个数据集上的泛化性能检验
我们有多大把握相信两个模型的泛化性能无显著差别?
# 1.9.2.1 交叉验证t检验
对两个模型A和B,各使用k折交叉验证分别得到k个测试错误率,即$\hat{\epsilon}_1^A$,$\hat{\epsilon}_2^A$, ... ,$\hat{\epsilon}_k^A$ 和 $\hat{\epsilon}_1^B$,$\hat{\epsilon}_2^B$, ... ,$\hat{\epsilon}_k^B$。使用k折交叉验证成对t检验(paired t-tests)来进行比较检验。
对于这两组k个测试错误率,计算两组之间的每一对的差,即 $\triangle_i = \hat{\epsilon}_k^A - \hat{\epsilon}_k^B$,从而得到k个 $\triangle$。我们可以计算 $\triangle$ 的均值 $\mu$ 和方差 $\sigma^2$,定义统计量t:
$$t = \lvert \frac{\sqrt{k}\mu}{\sigma} \rvert$$
可以看到,和前面的t检验相比,这里的分子没有被减项,其实是省略了。因为我们假设两个模型的泛化错误率相同,实际上是假设 $\lvert \epsilon^A - \epsilon^B \rvert = 0$,这个 $0$ 被省略了。
类似地,这个统计量服从自由度 $v = k-1$ 的t分布。我们设定好显著度 $\alpha$,查表获取临界值范围,如果计算出的t统计量落在在范围内,就能以$1-\alpha$ 的把握认为假设成立,即两个模型的泛化性能无显著差别,否则认为平均测试错误率较低的模型更胜一筹。
# 1.9.2.2 McNemar检验
对于一个二分类问题,如果使用留出法,我们不仅可以获得两个算法A和B各自的测试错误率,或能够获得它们分类结果的差别(都预测正确、都预测错误、一个预测正确一个预测错误),构成一张列联表(contingency table):
| 算法B | 算法A | |
|---|---|---|
| 分类正确 | 分类错误 | |
| 分类正确 | $e_{00}$ | $e_{01}$ |
| 分类错误 | $e_{10}$ | $e_{11}$ |
假设两个算法的泛化性能无显著区别,则 $e_{01}$ 应该等于 $e_{10}$,变量 $\lvert e_{01}-e_{10} \rvert$ 应服从均值为 $1$,方差为 $e_{01} + e_{10}$ 的正态分布,可以计算统计量 $\chi^2$:
$$\chi^2 = \frac{(\lvert e_{01}-e_{10} \rvert -1)^2}{e_{01} + e_{10}}$$
该变量服从自由度为 $v=1$ 的 $\chi^2$ 分布(卡方分布),类似t检验,设定好显著度 $\alpha$,按照自由度和显著度查表获得临界值。若计算所得的统计量 $\chi^2$ 小于临界值,则能以$1-\alpha$ 的把握认为假设成立,即两个算法的泛化性能无显著差别,否则认为平均测试错误率较低的算法更胜一筹。
注:这里 $v$ 为1是因为只有2个算法
1.9.3 多个模型/算法、多个数据集上的泛化性能检验
我们有多大把握相信多个模型的泛化性能皆无显著差别?若有,接下来怎样做?
在一组数据集上进行多个算法的比较,情况就变得较复杂了,一种做法是使用前面的方法分开两两比较;另一种更直接的做法是使用基于算法排序的Friedman检验。
# 1.9.3.1 Friedman检验
假设有 $N=4$ 个数据集,$k=3$ 种算法,可以使用一种评估方法,获得各个算法在各个数据集上的测试结果,然后按照性能度量由好到坏进行排序,序值为1,2,3。若并列,则取序值的平均值。然后对各个算法在各数据集上的序值求平均得到平均序值,如:
| 数据集 | 算法A | 算法B | 算法C |
|---|---|---|---|
| D1 | 1 | 2 | 3 |
| D2 | 1 | 2.5 | 2.5 |
| D3 | 1 | 2 | 3 |
| D4 | 1 | 2 | 3 |
| 平均序值 | 1 | 2.125 | 2.875 |
令 $r_i$ 表示第 $i$ 个算法的平均序值,则 $r_i$ 服从均值为 $\frac{k+1}{2}$,方差为 $\frac{(k^2)-1}{12}$ 的正态分布。可以计算统计量 $\chi^2$:
$$\chi^2 = \frac{12N}{k(k+1)}(\sum_{i=1}^k r_i^2 - \frac{k(k+1)^2}{4})$$
在 $k$ 和 $N$ 都较大时(通常要求 $k>30$),该变量服从自由度为 $v=k-1$ 的 $\chi^2$ 分布(卡方分布)。
以上这种检验方式也称为原始Friedman检验,被认为过于保守,现在通常用统计量 $F$ 代替:
$$F = \frac{(N-1)\chi^2}{N(k-1)-\chi^2}$$
该变量服从于自由度为 $v=k-1$ 或 $v=(k-1)(N-1)$ 的 $F$ 分布。
和前面的检验方式有所区别,F检验是根据设定的显著度 $\alpha$ 和算法个数 $k$ 以及 数据集个数$N$ 这三者来查表的,如果计算出的统计量 $F$ 小于查表所得的临界值,则假设成立,能以$1-\alpha$ 的把握认为认为这 $k$ 个算法的泛化性能无显著区别。
但如果这个假设被拒绝了呢?这时就需要进行后续检验(post-hoc test),常用的有 Nemenyi后续检验。
# 1.9.3.2 Nemenyi后续检验
定义平均序值差别的临界值域为:
$$CD = q_\alpha \sqrt{\frac{k(k+1)}{6N}}$$
其中 $q_\alpha$是由 显著度 $\alpha$ 和算法个数 $k$ 确定的,通过查表获取。若两个算法的平均序值之差不超过 $CD$,则能以$1-\alpha$ 的把握认为这两个算法的泛化性能无显著区别,否则认为平均序值较小的更胜一筹。
Nemenyi后续检验还可以通过Friedman检验图更直观地体现出来,横轴为性能度量,纵轴为算法,每个算法用一段水平线段表示,线段中心点为该算法的平均序值,线段长度为 $CD$。若两个算法的线段投影到x轴上有重叠部分,则可以认为这两个算法的泛化性能无显著区别。
1.10 相关学习资源
Conference 会议
International Conference on Data Mining
International Conference on Data Engineering
International Conference on Machine Learning
International Joint Conference on Artificial Intelligence
Pacific-Asia Conference on Knowledge Discovery and Data Mining
ACM SIGKDD Conference on Knowledge Discovery and Data Mining
Stars知名学者
Xindong Wu (吴信东)
Zhihua Zhou(周志华)
Jiawei Han
Jian Pei
Changshui Zhang
Philip S. Yu
Chih-Jen Lin
Qiang Yang
2. 数据预处理
2.1 缺失数据的处理
自动填充/手动填充?
1.忽略
2. 人工填写缺失值
3. 使用一个全部变量填充缺失值
填写 "Unknow"
4. 使用属性的中心度量(如均值或中位数)填充
5. 最可能的数据填充
ignore?
More art than science
2.2 异常值与重复数据检测
2.2.1 异常值检验的目的
找出数据集中和大多数数据不同的数据
2.2.2 异常值检验的主要方法
异常值检验主要方法有3种:
| 类型 | 详解 | 示例 |
|---|---|---|
| 基于统计学的方法 | 这种方法一般会构建一个概率分布模型,并计算对象符合该模型的概率,把具有低概率的对象视为异常点 | 特征工程中的RobustScaler方法 |
| 基于聚类方法 | 基于数据特征的分布来做的 | BIRCH聚类算法原理、DBSCAN密度聚类 |
| novelty detection | 当训练数据中没有离群点,我们的目标是用训练好的模型去检测另外新发现的样本 | OneClassSVM |
| outlier detection | 当训练数据中包含离群点,模型训练时要匹配训练数据的中心样本,忽视训练样本中的其它异常点 | Isolation Forest(低维度)、Local Outlier Factor(中高纬度) |
1. RobustScaler
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.robust_scale.html
对数据集进行升序排列,取数据集中间 quantile_range 范围的数据
sklearn.preprocessing.robust_scale(X, axis=0, with_centering=True, with_scaling=True, quantile_range=(25.0, 75.0), copy=True
2. OneClassSVM
http://scikit-learn.org/stable/auto_examples/svm/plot_oneclass.html
- 属于支持向量机大家族
- 无监督学习的方法
支持向量机的边界(支持向量) 一边为无穷远,一边为球的外边缘,求最大间隔。间隔外的数据为异常值 ,间隔内的数据为正常值
在sklearn中,我们可以用svm包里面的OneClassSVM来做异常点检测。OneClassSVM也支持核函数,所以普通SVM里面的调参思路在这里也适用。
3. Isolation Forest
- 集成学习的思路
- 随机森林大家族的一员
- 周志华老师的学生提出
- 不适用于特别高维的数据
- 它具有线性时间复杂度
- 快速分到了叶子节点的数据 判定为 异常值
简介:
孤立森林(Isolation Forest)是另外一种高效的异常检测算法,它和随机森林类似,但每次选择划分属性和划分点(值)时都是随机的,而不是根据信息增益或者基尼指数来选择。在建树过程中,如果一些样本很快就到达了叶子节点(即叶子到根的距离d很短),那么就被认为很有可能是异常点。因为那些路径d比较短的样本,都是因为距离主要的样本点分布中心比较远的。也就是说,可以通过计算样本在所有树中的平均路径长度来寻找异常点。
示例:
sklearn.ensemble.IsolationForest(n_estimators=100, max_samples=’auto’, contamination=0.1, max_features=1.0, bootstrap=False, n_jobs=1, random_state=None, verbose=0)
参数:
n_estimators : int, optional (default=100)森林中树的颗数 max_samples : int or float, optional (default=”auto”)对每棵树,样本个数或比例 contamination : float in (0., 0.5), optional (default=0.1) 这是最关键的参数,用户设置样本中异常点的比例 max_features : int or float, optional (default=1.0) 对每棵树,特征个数或比例
函数:
fit(X) Fit estimator.(无监督) predict(X) 返回值:+1 表示正常样本, -1表示异常样本。 decision_function(X) 返回样本的异常评分。 值越小表示越有可能是异常样本。
4. 局部异常因子算法 LOF
- 中等高维数据集上执行异常值检测
- 基于密度的算法
算法简介:
https://blog.csdn.net/bbbeoy/article/details/80301211
了解了 LOF 的定义,整个算法也就显而易见了:
1. 对于每个数据点,计算它与其它所有点的距离,并按从近到远排序;
2. 对于每个数据点,找到它的 k-nearest-neighbor,计算 LOF 得分。
-
K-邻近距离(k-distance)
k-distance (o)
在距离数据点 o 最近的几个点中,第 k 个最近的点跟点 O 之间的距离称为点 p 的 K-邻近距离,记为k-distance (o) -
可达距离(rechability distance)
reach_dist_k
可达距离的定义跟K-邻近距离是相关的,给定参数k时, 数据点 p 到 数据点 o 的可达距离 reach-dist(p, o)为数据点 o 的K-邻近距离 和 数据点p与点o之间的直接距离的最大值。
$$reach_dist_k(p,o)=max{k_distance(o),d(p,o)}$$
- 局部可达密度(local rechability density):
数据点 p 的局部可达密度为它与邻近的数据点的平均可达距离的倒数,即:
$$lrd_k(p)=\frac{1}{\frac{\sum_{o\in{N_{k}(p)}}reach_dist_k(p,o)}{|N_k(p)|}}$$
局部异常因子(local outlier factor):根据局部可达密度的定义,如果一个数据点跟其他点比较疏远的话,那么显然它的局部可达密度就小。但LOF算法衡量一个数据点的异常程度,并不是看它的绝对局部密度,而是看它跟周围邻近的数据点的相对密度。这样做的好处是可以允许数据分布不均匀、密度不同的情况。局部异常因子即是用局部相对密度来定义的。数据点 p 的局部相对密度(局部异常因子)为点p的邻居们的平均局部可达密度跟数据点p的局部可达密度的比值,即:
$$LOF_{k}(p)=\frac{\sum_{o\in{N_k(p)}}\frac{lrd(o)}{lrd(p)}}{|N_{k}(p)|}=\frac{\sum_{o\in{N_{k}(p)}}lrd(o)}{|N_{k}(p)|}/lrd(p)$$
根据局部异常因子的定义,如果数据点 p 的 LOF 得分在1附近,表明数据点p的局部密度跟它的邻居们差不多;如果数据点 p 的 LOF 得分小于1,表明数据点p处在一个相对密集的区域,不像是一个异常点;如果数据点 p 的 LOF 得分远大于1,表明数据点p跟其他点比较疏远,很有可能是一个异常点。下面这个图来自 Wikipedia 的 LOF 词条,展示了一个二维的例子。上面的数字标明了相应点的LOF得分,可以让人对LOF有一个直观的印象。
Local Outlier Factor主要参数和函数介绍
sklearn.neighbors.LocalOutlierFactor(n_neighbors=20, algorithm=’auto’, leaf_size=30, metric=’minkowski’, p=2, metric_params=None, contamination=0.1, n_jobs=1)
1)主要参数
- n_neighbors : 设置k,default=20
- contamination :设置样本中异常点的比例,default=0.1
2)主要属性:
- negative_outlier_factor_ : numpy array, shape (n_samples,)和LOF相反的值,值越小,越有可能是异常点。(注:上面提到LOF的值越接近1,越可能是正常样本,LOF的值越大于1,则越可能是异常样本)。这里就正好反一下。
3)主要函数:
1. fit_predict(X)
X : array-like, shape (n_samples, n_features)
2.3 类型转换与采样
2.3.1 类型转换
通常的数据类型包括:
1. 连续型数据
- 区间标度
Real values: Temperature, Height, Weight … - 比例标度
百分比
处理方法:
二值化与分段
sklearn.preprocessing.Binarizer 根据阈值将数据二值化(将特征值设置为0或1),用于处理连续型变量。大于阈值的值映射为1,而小于或等于阈 值的值映射为0。默认阈值为0时,特征中所有的正值都映射到1。二值化是对文本计数数据的常见操作,分析人员 可以决定仅考虑某种现象的存在与否。它还可以用作考虑布尔随机变量的估计器的预处理步骤(例如,使用贝叶斯 设置中的伯努利分布建模)。
2. 离散数据
Integer values: Number of people …
3. 有序数据
排名 Rankings: {Average, Good, Best}, {Low, Medium, High} …
4.名词性质的数据
标签 Symbols: {Teacher, Worker, Salesman}, {Red, Green, Blue} …
5.字符串
Text: “Tsinghua University”, “No. 123, Pingan Avenue” …
处理方法:
one-hot
embedding
6.无序数据
ID:{1001,1002}
2.3.2 特征缩放 Feature scaling
1.数据归一化 Normalization/重新缩放 Rescaling (min-max normalization)
$$x^{new}=\frac{x-x_{min}}{x_{max}-x_{min}}$$
from sklearn.preprocessing import MinMaxScaler #归一化 MinMaxScaler().fit_transform(iris.data)
2.标准化 Standardization
做数据标准化(Standardization,又称Z-score normalization),公式如下:
$$x^{new}=\frac{x-x_{mean}}{\sigma}$$
from sklearn.preprocessing import StandardScaler #标准化,返回值为标准化后的数据 StandardScaler().fit_transform(iris.data)
3.均值归一化 Mean normalization
$$x^{new}=\frac{x-x_{mean}}{x_{max}-x_{min}}$$
2.3.2 采样
- 通过对数据集采样降低时间复杂度
- 过采样/欠采样 解决数分布不均的问题class-imbalance
1. 欠采样
EasyEnsemble (周志华)
https://imbalanced-learn.org/en/stable/generated/imblearn.ensemble.EasyEnsemble.html
2. 过采样
SMOTE 算法
参考:https://arxiv.org/abs/1106.1813
https://www.jianshu.com/p/13fc0f7f5565
JAIR'2002的文章《SMOTE: Synthetic Minority Over-sampling Technique》提出了一种过采样算法SMOTE
本算法基于“插值”来为少数类合成新的样本。下面介绍如何合成新的样本。
设训练集的一个少数类的样本数为 T ,那么SMOTE算法将为这个少数类合成 NT 个新样本。这里要求 N 必须是正整数,如果给定的 N<1 那么算法将“认为”少数类的样本数 $T=NT$ ,并将强制 $N=1$ 。
考虑该少数类的一个样本 i ,其特征向量为 $xi,i∈{1,...,T}$ :
-
首先从该少数类的全部 T 个样本中找到样本 xi 的 k 个近邻(例如用欧氏距离),记为 xi(near),near∈{1,...,k} ;
-
然后从这 k 个近邻中随机选择一个样本 xi(nn) ,再生成一个 0 到 1 之间的随机数 ζ1 ,从而合成一个新样本 xi1 :
$$xi1=xi+ζ1⋅(xi(nn)−xi)$$
- 将步骤2重复进行 N 次,从而可以合成 N 个新样本:xinew,new∈1,...,N。
那么,对全部的 T 个少数类样本进行上述操作,便可为该少数类合成 NT 个新样本。
如果样本的特征维数是 2 维,那么每个样本都可以用二维平面上的一个点来表示。SMOTE算法所合成出的一个新样本 xi1 相当于是表示样本 xi 的点和表示样本 xi(nn) 的点之间所连线段上的一个点。所以说该算法是基于“插值”来合成新样本。
SMOTE算法的缺陷
1. 是在近邻选择时,存在一定的盲目性。从上面的算法流程可以看出,在算法执行过程中,需要确定K值,即选择多少个近邻样本,这需要用户自行解决。从K值的定义可以看出,K值的下限是M值(M值为从K个近邻中随机挑选出的近邻样本的个数,且有M< K),M的大小可以根据负类样本数量、正类样本数量和数据集最后需要达到的平衡率决定。但K值的上限没有办法确定,只能根据具体的数据集去反复测试。因此如何确定K值,才能使算法达到最优这是未知的。
2. 另外,该算法无法克服非平衡数据集的数据分布问题,容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻,如果一个负类样本处在负类样本集的分布边缘,则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘,且会越来越边缘化,从而模糊了正类样本和负类样本的边界,而且使边界变得越来越模糊。这种边界模糊性,虽然使数据集的平衡性得到了改善,但加大了分类算法进行分类的难度.
改进
针对SMOTE算法的进一步改进针对SMOTE算法存在的边缘化和盲目性等问题,很多人纷纷提出了新的改进办法,在一定程度上改进了算法的性能,但还存在许多需要解决的问题。
- Han等人Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning在SMOTE算法基础上进行了改进,提出了Borderhne.SMOTE算法,解决了生成样本重叠(Overlapping)的问题该算法在运行的过程中,查找一个适当的区域,该区域可以较好地反应数据集的性质,然后在该区域内进行插值,以使新增加的“人造”样本更有效。这个适当的区域一般由经验给定,因此算法在执行的过程中有一定的局限性。
2.4 数据描述与可视化
2.4.1 中心趋势
| 指标 | 描述 |
|---|---|
| 均值 | |
| 中位数 | |
| 众数 | |
| #### 2.4.2 离散 | |
| 指标 | 描述 |
| -----: | ---: |
| 方差 | |
| 极差 | |
| 标准差 | |
| 分位数 |
2.5 特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
- Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
- Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
- Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
我们使用sklearn中的feature_selection库来进行特征选择。
2.6 主成分分析(PCA)
推荐参考 https://zhuanlan.zhihu.com/p/77151308
2.7 线性判别分析(LDA)
3. 从贝叶斯到决策树
后验概率朴素贝叶斯
3.1 贝叶斯奇幻之旅
3.2 朴素是一种美德
朴素贝叶斯(NB)
3.3 数据、规则与树
决策->决策树
为了要将表格转化为一棵树,决策树需要找出最佳节点和最佳的分枝方法,对分类树来说,衡量这个“最佳”的指标 叫做“不纯度”
3.4 植树造林学问大
4. 神经网络
略
5. 支持向量机
5.1 最大间隔
- 支持向量
- 间隔
- KKT条件是指在满足一些有规则的条件下, 一个非线性规划(Nonlinear Programming)问题能有最优化解法的一个必要和充分条件.
5.2 线性SVM
- 软间隔
- noise
5.3 Kernel Trick
- 非线性问题 导致 高计算资源消耗
- Kernel Trick 解决
$$ K(xi,xj) = φ(xi)·φ(xj) $$
6. 聚类分析:物以类聚
聚类是机器学习中的“新算法”,一个重要的原因是聚类不存在客观标准,给定数据集总能从不同角度找到以往算法未能覆盖的某种标准。
6.1 无监督学习
6.1.1 无监督学习特点:
- 没有标签
- 数据驱动
6.1.2 无监督学习的 簇 cluster特点:
- 同一类样本距离 越近
- 不同类的样本 距离越远
| 指标(中文) | 指标(En) | 期望 |
|---|---|---|
| 簇内相似度 | intra cluster similarity | 高 |
| 簇间相似度 | inter cluster similarity | 低 |
6.1.3 无监督学习的应用:
- Market Research 市场检索
- Image Segmentation 图像分类
- Social Network Analysis 社交网络分析
6.1.4 需求:
- 可扩展性(Scalability)
- 处理不同类型属性的能力(Ability to deal with different types of attributes)
- 能够发现任意形状的集群(Ability to discover clusters with arbitrary shape)
- 对领域知识的最低要求(Minimum requirements for domain knowledge)
- 处理噪音和异常值的能力(Ability to deal with noise and outliers)
- 对输入记录顺序不敏感(Insensitivity to order of input records)
- 合并用户定义的约束(Incorporation of user-defined constraints)
- 可解释性和可用性(Interpretability and usability)
6.1.5 聚类性能评价
聚类性能评价分为2类:
6.1.5.1 外部指标(与某个参考模型比较)
数据集 $D={x_1,x_2,x_3 ... x_n}$
通过聚类得到的模型分了m个簇,m个簇的集合$C={c_1,c_2,..c_m}$
通过外面分了s个簇,s个簇的集合$C^={c^_1,c^_2,..c^_s}$
从D中找到1 样本对$ (x_i,x_j) $
| 指标 | en | 计算 | 含义 |
|---|---|---|---|
| Jaccard 系数 | Jaccard Coefficient,JC | $$ JC=\frac a | 越大越好 |
| FM指数 | Fowlkes and Mallows index,FMI | $$FMI=\sqrt | 越大越好 |
| Rand 指数 | RI, Rand index | $$FMI=\frac | 越大越好 |
6.1.5.2 内部指标 (直接考察聚类结果)
| 指标 | en | 计算 | 含义 |
|---|---|---|---|
| DB 指数 | Davies-Bouldin Index,DBI | 越小越好 | |
| Dunn 指数 | Dunn index,DI | 越大越好 | |
| Rand 指数 | RI, Rand index | 越大越好 | |
| 轮廓系数 | Silhouette Coefficient | $$a(i) = average(i向量到所有它属于的簇中其它点的距离)$$ ; $$ b(i) = min (i向量到各个非本身所在簇的所有点的平均距离)$$ $$ S=\frac | si接近1,则说明样本i聚类合理; si接近-1,则说明样本i更应该分类到另外的簇; 若si 近似为0,则说明样本i在两个簇的边界上。 |
6.1.5 距离计算
-
度量的相异度具有3个性质:
- 非负性(距离为非负数)
- 对称性(A->B==B->A)
- 三角不等式(A->C->B != A->B)
例如:A点到B点的距离
-
非度量的相异度
不满足度量的相异度具有3个性质的距离
例如:时间点A与时间点B的时间间隔
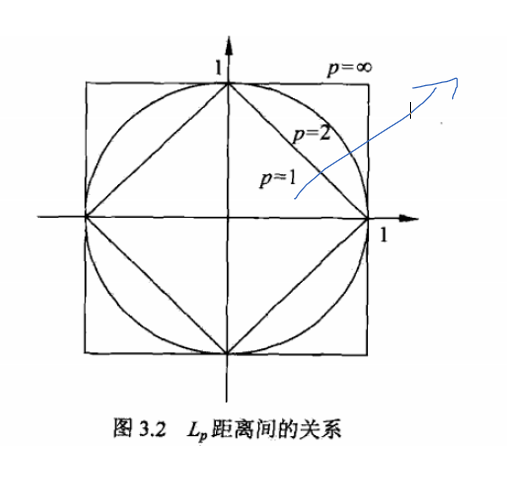
6.1.5.1 明式距离(有序属性)
明可夫斯基距离(Minkowski Distance)
* 可用于有序属性
$$ dist(xi,xj)=(\sum^n_{u=1} |x_{iu}-x_{ju} |^p)^{1\over p} $$
6.1.5.1.1 欧式距离(Euclidean Distance)
当$p=2$时
$$ dist(xi,xj)=(\sum^n_{u=1} |x_{iu}-x_{ju} |^2)^{1\over 2} $$
6.1.5.1.2 曼哈顿距离(Mahalanobis Distance)
当$p=1$时
$$ dist(xi,xj)=(\sum^n_{u=1} |x_{iu}-x_{ju} |) $$
6.1.5.2 VDM距离(无序属性)
$$VDM_p(a,b)=\sum^k_{i=1} {| \frac {m_{u,a,i}} {m_{u,a}} -\frac {m_{u,b,i}} {m_{u,b}}|}$$
$m_{u,a}$ 属性u在取值为a的样本数
$m_{u,a,i}$ 在第i个样本 属性u在取值为a的样本数
6.1.5.3 MINKOVDM距离(无序+有序属性)
$$ {MINKOVDM}(xi,xj)=(\sum^n_{u=1} |x_{iu}-x_{ju} |^p)^{1\over p}+\sum^k_{i=1} {| \frac {m_{u,a,i}} {m_{u,a}} -\frac {m_{u,b,i}} {m_{u,b}}|})$$
6.1.5.4 加权距离(无序+有序属性)
6.1.5.5 马氏距离
表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法
$$sqrt( (x-μ)'Σ^(-1)(x-μ) )$$
6.1.5.6 非度量距离
6.1.6 不同的聚类类型
6.1.6.1 按数据点的排他性
- Exclusive Clustering 互斥聚类(K-means,LVQ)
也就是这个点,要么是属于你的,要么属于我的,我们两个群组不能共同包含这个点
- Overlapping Clustering 重叠聚类 (Fuzzy K-means)
这种聚类方法引入了一种模糊集合(fuzzy sets)概念,所以,一个点可以同时属于多个群组。
6.1.6.2 按簇集合性质
- 划分聚类(partitional clustering)
簇集合是非嵌套的、划分的 - 层次聚类(Hierarchical clustering)
簇集合是层次的,嵌套的
6.1.6.3 按数据划分的完全性
- 完全聚类(complete clustering)
所有数据点都有明确的簇 - 部分聚类(partial clustering)
存在离群点、噪音,没有明确的簇
6.1.7 不同的簇类型
| 类型 | 描述 |
|---|---|
| 分离明显的 | 任意形状,分离明显 |
| 基于原型的 | 大部分情况可以认为是基于中心的簇(center-based cluster),簇趋向于呈球状 |
| 基于图的 | 簇定义为连通分支(connected component),即簇内对象相互连通,不与组外对象连通的对象组 |
| 基于密度 | ·· |
| 共同性质的(概念簇) | ·· |
6.1.7.1 分离明显的簇
- 任意形状
- 簇内距离远小于簇间距离
6.1.7.2 基于原型的簇
原型是指样本空间中具有代表性的点
| 数据类型 | 簇的原型 |
| -------: | -------------------------: |
| 连续属性 | 质心,即族中所有点的平均值 |
| 分类属性 | 中心点,簇中最有代表性的点 |
当原型为最靠近中心的点时,可把基于原型的簇看作 基于中心的簇(center-based cluster)
6.1.7.3 基于图的簇
当数据结果为图的结果时(节点:对象;边:对象之间的联系)
6.1.7.4 基于密度的簇
簇是对象的稠密区域被低密度区域环绕
6.1.7.5 共同性质的簇(概念簇)
把簇定义为具有某种共同性质的对象的集合
按算法类型分:
1. 原型聚类(protoype-based clustering)
原型聚类是指聚类结构能通过一组原型刻画。
特点:
1. 发现球形互斥的簇
2. 基于距离
3. 可用均值或中心点代表簇中心
4. 对中小规模数据有效
1.1 k-mean
- 无标记
- 均值
- 利用原型向量
1.2 LVQ (Learning-Vector Quantization)学习向量化
- 有标记
- 利用原型向量
1.3 高斯混合 --概率 基于模型 的聚类
- 利用概率模型
2. 层次聚类(Hierarchical clustering)
思路是先把每个点都看作一个cluster,然后再把最近的两个cluster聚合成为一个新的cluster,如此这般,不断迭代,直到满足最后设定的要求。
特点:
1. 聚类是一个层次分解
2. 不能纠正错误的合并或划分
3. 可以集成其他技术
具体算法:
1. AGNES(AGglomerative NESting的缩写)
3. 密度聚类(Density-based clustering)
基于数据密度,不需要确定k值。
特点:
1. 可以发现任意形状的簇
2. 簇是对象空间中被低密度区域分隔的稠密区域
3. 簇密度
4. 可能过滤离群点
具体算法:
1. DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
6.2 K-Means
- 基于原型的、划分的 聚类技术
K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,
因此 K-均值的代价函数(又称畸变函数 Distortion function)为:
6.2.1 主要思想
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的居民,于是每个居民到离自己家最近的布道点去听课。听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的居民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个居民又去了离自己最近的布道点……就这样,牧师每个礼拜更新自己的位置,居民根据自己的情况选择布道点,最终稳定了下来。
6.2.2 应用场景
| 应用场景 | 描述 |
|---|---|
| 矢量的量化 | 在计算机图形学中,色彩量化的任务,就是要把一张图像的色彩范围减少到一个固定的数目k上来 |
| 聚类分析 | 在聚类分析中,k-均值算法被用来将输入数据划分到k个部分(聚类)中 |
| 特征学习 | 在(半)监督学习或无监督学习中,k-均值聚类被用来进行特征学习(或字典学习)步骤。 |
6.2.3 损失函数
如果距离度量算做损失的话,欧式距离为平方损失。
6.2.3 主要推导
K-means是为了求解如下公式,其中$$S = {S_1,S_2,...,S_n}$$表示n个聚类后的类别。
$$ \mathop {\arg \min }\limits_S \sum\limits_{i = 1}^k {\sum\limits_{j \in {S_i}}^{} {||{x_j} - {\mu _{{S_i}}}|{|^2}} } $$
在一般欧式空间中,即使是两个簇,这个问题是NP难问题,即使在二维欧式空间,对一般的簇个数k,该问题也是NP难的。K-means使用贪心算法,通过迭代的方式克服计算中的巨大开销。
Tips:
NP问题:(非确定性多项式,non-deterministic polynomial,NP)问题
如果一个问题可以找到一个能在多项式的时间里解决它的算法,那么这个问题就属于P问题。NP问题不是非P类问题。NP问题是指可以在多项式的时间里验证一个解的问题。NP问题的另一个定义是,可以在多项式的时间里猜出一个解的问题。NPC问题的定义非常简单。同时满足下面两个条件的问题就是NPC问题。首先,它得是一个NP问题;然后,所有的NP问题都可以约化到它。NP-Hard问题是这样一种问题,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比NPC问题的范围广)。
求解算法:
1. 随机选取初始聚类中心
2. 通过计算距离进行聚类
3. 重新计算聚类中心
4. 重复2-3步直至聚类中心不发生改变或者达到迭代次数上限
伪代码
输入:数据集D(N个样本),聚类簇数K 过程: 从D中随机选择K个向量做聚类中心 repeat 初始化聚类结果集为空集 for j = 0...N do 计算样本与均值向量的距离,将其划归为对应的类别 end for for 使用均值法重新计算聚类中心 end for until 聚类中心均不发生改变或者达到指定迭代次数T 输出:聚类结果集
复杂度分析
T迭代次数,N样本数,m样本维数,K聚类中心数
时间复杂度:$O(TNmK)$
空间复杂度: $O((m+K)N)$
6.2.4 大数据下改进
mahout中对K-means的具体实现* spark Mlib中对K-means的实现
第一步:Map:对于每一个点,将其分配到最近的聚类中心
第二步:Combine:刚完成map的机器在本机上都分别完成同一个聚类的点的求和,减少reduce操作的通信量和计算量。
第三步:reduce:将同一聚类中心的中间数据再进行求和,得到新的聚类中心。
优点:
1. 速度快,复杂度与样本数线性相关,即使在大数据下依旧保持良好效果
缺点:
1. 聚类数目K是一个输入参数。选择不恰当的K值可能会导致糟糕的聚类结果。这也是为什么要进行特征检查来决定数据集的聚类数目了。
2. 收敛到局部最优解,可能导致“反直观”的错误结果。
3. k-均值算法的一个重要的局限性即在于它的聚类模型。这一模型的基本思想在于:得到相互分离的球状(各项同性)聚类,在这些聚类中,均值点趋向收敛于聚类中心。 一般会希望得到的聚类大小大致相当,这样把每个观测都分配到离它最近的聚类中心(即均值点)就是比较正确的分配方案。但遇到椭球或不规则数据可能会发生问题。
K如何确定?
1. 使用层次聚类确定
2. 初始质心的选取
K-means++
算法中的距离不一定是欧式距离,可以自由定义任意符合距离定义要求的"距离"
关键领悟
K-Means can be seen as a special case of Gaussian mixture model with equal covariance per component.??
K-means is equivalent to the expectation-maximization algorithm with a small, all-equal, diagonal covariance matrix.
这样从K-means里我们可以看出它其实就是EM的体现,E步是确定隐含类别S变量类别,M步更新其他参数$\mu$中心来使J最小化。这里的隐含类别变量指定方法比较特殊,属于硬指定,从K个类别中硬选出一个给样例,而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程,有目标函数,也有参数变量,只是多了个隐含变量,确定其他参数估计隐含变量,再确定隐含变量估计其他参数,直至目标函数最优。
K-Means采用了坐标下降法求解,先固定中心,优化类别,再固定类别,优化中心
The algorithm can also be understood through the concept of Voronoi diagrams.
6.3 期望最大法
6.3.1 高斯混合模型聚类
多个高斯模型混合
峰的个数和高斯模型的个数不同
最大化极大似然常采用EM算法。
6.3.1.1 EM 算法
用来寻找对数据集建模的高斯混合的算法称为EM (expectzation, Dempster, Laird and Rubin, 1977)。
最大期望算法(Expectation-maximization algorithm,又译期望最大化算法)
是常用的估计参数隐变量的利器
主要步骤:
E步(Expectation):以当前 参数 推断 隐变量分布
M步 (Maximization): 寻找最大化期望似然
模型有参数需求-> EM
现在我们总结下EM算法的流程。
输入:观察数据x=(x(1),x(2),...x(m)),联合分布p(x,z;θ), 条件分布p(z|x;θ), 最大迭代次数J。
1) 随机初始化模型参数$θ$的初值$θ_0$。
2) for j from 1 to J开始EM算法迭代:
a) E步:计算联合分布的条件概率期望:
$$Qi(z(i))=P(z(i)|x(i),θj))$$
$$L(θ,θj)=∑i=1m∑z(i)Qi(z(i))logP(x(i),z(i);θ)$$
b) M步:极大化L(θ,θj),得到θj+1:
$$θj+1=argmaxθL(θ,θj)$$
c) 如果θj+1已收敛,则算法结束。否则继续回到步骤a)进行E步迭代。
输出:模型参数θ。
6.4 密度与层次
6.4.1 基于密度的聚类
根据连通性的原则
DB-scan
6.4.1 基于层次的聚类
7. 关联规则
7.1 项集与规则
关联规则(Association Rules)学习
关联规则(Association Rules)是反映一个事物与其他事物之间的相互依存性和关联性,是数据挖掘的一个重要技术,用于从大量数据中挖掘出有价值的数据项之间的相关关系。
常见的购物篮分析
该过程通过发现顾客放人其购物篮中的不同商品之间的联系,分析顾客的购买习惯。通过了解哪些商品频繁地被顾客同时购买,这种关联的发现可以帮助零售商制定营销策略。其他的应用还包括价目表设计、商品促销、商品的排放和基于购买模式的顾客划分。
可从数据库中关联分析出形如“由于某些事件的发生而引起另外一些事件的发生”之类的规则
频繁项集评估标准
常用的频繁项集的评估标准有支持度,置信度和提升度三个
支持度:几个关联的数据在数据集中出现的次数占总数据集的比重
置信度:一个数据出现后,另一个数据出现的概率,或者说数据的条件概率。
提升度:表示含有Y的条件下,同时含有X的概率,与X总体发生的概率之比
关联分析的目标:
发现频繁项集:发现满足最小支持度的所有项集
发现关联规则:从频繁项集中提取所有高置信度的规
7.2 支持度与置信度
7.3 误区
7.4 Apriori 算法
Apriori算法----发现频繁项集的一种方法
原理:如果一个项集是频繁项集,则它的所有子集都是频繁项集
如果一个集合不是频繁项集,则它的所有父集(超集)都不是频繁项集
8. 推荐算法:察言观色,投其所好
8.1 无所不在的推荐(略)
8.2 隐含语义分析
8.3 PageRank传奇
8.4 协同过滤 (Collaborative Filtering, 简称 CF)
4 协同过滤的实现
要实现协同过滤的推荐算法,要进行以下三个步骤:
4.1 收集数据
4.2 找到相似用户和物品
4.3 进行推荐
相似度
8.5 告诉你一个真实的推荐
9.集成学习:兼听则明,偏听则暗
集成学习(Ensemble,发音:嗯森波 不是应森波)不是一个算法,是一大类算法。
集成学习(ensemble learning)通过构建并结合多个学习期来完成学习任务,有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning) 等。
集成学习主要有 Bagging\Boosting 两类:
9.1 Bagging (Bootstrap Aggregating)
Bagging :bag 袋子,Bagging 袋装法
- 多个分类器并行
- 数据 Bagging sampling(有放回的抽样)
9.1.1 随机森林 (Random Forest,RF)
9.2 Boosting (提升方法)
多个分类器串行 Stacking->Boosting
梯度下降法(Gradient Descent,GD)算法是求解最优化问题最简单
9.2.1 提升树(Boosting Tree)
以决策树(Decision Tree)为分类器的提升方法成为提升树,提升树模型可以表示为决策树的加法模型
| 决策树类型 | 解决问题 |
|---|---|
| 二叉分类树 | 分类问题 |
| 二叉回归树 | 回归问题 |
| 分类回归树(Classification and Regression Tree,CART) | 分类+回归问题 |
9.2.1.1 基于 二叉分类树 的 提升树
9.2.1.2 基于 回归树 的 提升树
在构建回归树时,主要有两种不同的树:
| 分类器 | 描述 |
|---|---|
| 回归树(Regression Tree) | 其每个叶节点是单个值 |
| 模型树(Model Tree) | 其每个叶节点是一个线性方程 |
9.2.1.2.1 梯度提升决策树(Gradient Boosting Decision Tree,GBDT)
注意:GDBT中所的DT(Decision Tree)树都是回归树而不是分类树,所以GDBT也叫MART(Multiple Additive Regression Tree)、GBRT(Gradient Boost Regression Tree)。下面主要叙述回归问题的提升树。
GBDT的核心就在于,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁,但第一棵树的预测年龄是12岁,差了6岁,即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习,如果第二棵树真的能把A分到6岁的叶子节点,那累加两棵树的结论就是A的真实年龄;如果第二棵树的结论是5岁,则A仍然存在1岁的残差,第三棵树里A的年龄就变成1岁,继续学。这就是Gradient Boosting在GBDT中的意义
9.2.1.1 基于 分类回归树 CART 的 提升树
在梯度提升决策树GBDT中,通过定义不同的损失函数,可以完成不同的学习任务,二分类是机器学习中一类比较重要的分类法,在二分类中,其损失函数为:
$$L(y,F)=log(1+exp(−2yF)),y∈{−1,1}$$
对于连续型的问题,我们可以使用方差的概念来表达混乱程度,方差越大,越紊乱。所以我们要找到使得切分之后的方差最小的划分方式。
9.2.2 AdaBoost
理论上可以选择任何一个分类或者回归学习器,不过需要支持样本权重。
我们常用的一般是CART决策树或者神经网络MLP。默认是决策树,即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier,而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor。
| 分类器 | 描述 |
|---|---|
| CART分类树 | AdaBoostClassifier 默认使用 |
| CART回归树 | AdaBoostRegressor 默认使用 |
| 神经网络MLP | 可以用 |
Advantages
Simple and easy to implement
Almost no parameters to tune
Proven upper bounds on training set
Immune to overfitting
Disadvantages
Suboptimal 𝛼 values
Steepest descent
Sensitive to noise
9.2.3 RegionBoost
AdaBoost assigns fixed weights to models.
However, different models emphasize different regions.
The weights of models should be input-dependent.
Given an input, only invoke appropriate models.
Train a competency predictor for each model.
Estimate whether the model is likely to make a right decision.
Use this information as the weight.
Maclin, R.: Boosting classifiers regionally. AAAI, 700-705, 1998.
10. 进化计算
10.1 人与自然
进化计算(EA)是一类算法
包括
10.2 尽善尽美
目标函数 Objective Function
问题列表:
1. Portfolio Optimization
2. Travelling Salesman Problem
3. Knapsack Problem
4. Bin Packing Problem
10.3 走向进化
10.4 遗传算法初探
10.5 遗传算法进阶
10.6 遗传程序设计
10.7 万物皆进化
10.8 相关学习资源
11. 其他1-懒惰学习
优点:
简单有效;对数据的分布没有要求;训练阶段很快。
缺点:
不产生模型,不建模,在发现特征之间的关系上的能力有限;分类阶段很慢;需要大量的内存;名义变量(特征)和缺失数据需要额外处理。
之所以被称为懒惰学习算法,是因为从技术上说,没有抽象化的步骤。抽象过程与一般过程都被跳跃过去了。由于高度依赖训练案例,所以懒惰学习又称为机械学习。机械学习不会建立一个模型,所以该方法被归类为非参数学习方法。
11.1 knn k-近邻分类
已知:带标签的训练集或者样本集 $ D={(x_1,y_1),(x_2,y_2)...(x_n,y_n)} $
需求:求未知标签的数据$T={(x_t)}$ 的标签 $y_t$
问题类型: 分类 ,对T 进行分类
过程:
1. 计算测试数据与各个训练数据之间的距离;
2. 按照距离的递增关系进行排序;
3. 选取距离最小的K个点;
4. 确定前K个点所在类别的出现频率;
5. 返回前K个点中出现频率最高的类别作为测试数据的预测分类。
KNN
分类算法
监督学习
数据集是带Label的数据
没有明显的训练过程,基于Memory-based learning
K值含义 - 对于一个样本X,要给它分类,首先从数据集中,在X附近找离它最近的K个数据点,将它划分为归属于类别最多的一类
K-means
聚类算法
非监督学习
数据集是无Label,杂乱无章的数据
有明显的训练过程
K值含义- K是事先设定的数字,将数据集分为K个簇,需要依靠人的先验知识
不同点:
两种算法之间的根本区别是,K-means本质上是无监督学习,而KNN是监督学习;K-means是聚类算法,KNN是分类(或回归)算法。
K-means算法把一个数据集分割成簇,使得形成的簇是同构的,每个簇里的点相互靠近。该算法试图维持这些簇之间有足够的可分离性。由于无监督的性质,这些簇没有任何标签。KNN算法尝试基于其k(可以是任何数目)个周围邻居来对未标记的观察进行分类。它也被称为懒惰学习法,因为它涉及最小的模型训练。因此,它不用训练数据对未看见的数据集进行泛化。
相似点:算法都包含给定一个点,在数据集中查找离它最近的点的过程。
关于为什么不用曼哈顿距离而是采用欧氏距离。主要是因为曼哈顿距离只计算水平和垂直距离,所以有维度的限制。欧氏距离可以用于任何空间距离的计算问题。由于数据点可能存在于任何空间,所以欧氏距离是更为可行的选择。
