1. 损失函数讨论

损失函数是衡量由特征值x经过模型f得到的预测值y_=f(x)与真实值y的差距，是衡量预测错误程度的指标

函数的问题最终还是要归结于任务类型，是处理 predict_label 和 real_label 的问题

单个样本：损失函数（Loss Function）
多个样本：成本函数（Cost Function）

目标函数（Object Function）：在有约束条件下的最小化成本函数，通常市经验损失(loss/cost)+结构损失(Ω)

经验损失(loss/cost)：就是传说中的损失函数或者代价函数。
结构损失(Ω)：就是正则项之类的来控制模型复杂程度的函数。
1. 离散数据
1. 分类
1. 二分类
2. 多分类
2. 连续数据
1. 回归

2. 分类损失

2.1. 0-1 损失函数

$$
Loss(y_ ,y)=\begin{cases}
1 (y_!=y)\
0 (y_==y)\
\end{cases}
$$

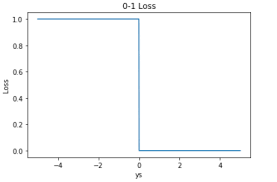
手动：

# real_label shape =(N,···)
# predict_label shape =(N,···)
# predict_label.shape==real_label.shape
loss = tf.cast(tf.equal(real_label, predict_label), tf.float32)
# loss shape =(N,1)
cost = tf.reduce_mean(loss)
# cost shape= ()  is a  val 数字

封装：

# 注意正确率的定义中 相等以及不等 相反,函数为不正确率 
tensorflow 无单独封装 ,可从tf.meteitc 正确率转换（但还不如手写来的快）

应用：
感知机

但是由于0-1损失函数相等这个条件太过严格，因此我们可以放宽条件，即满足时认为相等

$$Loss(y_ ,y)=\begin{cases}
1 (|y_ -y|>=error)\
0 (|y_ -y|<error)\
\end{cases}
$$

2.2. log对数函数（难点）

2.2.1. 关于概率的讨论

概率（Probability）
概率（Probability） P 描述的是某事件A出现的次数与所有事件出现的次数之比:

$$P(A)=\frac{发生事件A的次数}{发送所有事件的次数}$$

$$P(A) \subset[0,1]$$

几率（Odds）
如果针对二分类问题，事件A为正样本事件，将P(A)视为正样本的概率，则1-P(A)为负样本的可能性，形如下面的则称为事件为正样本的几率（Odds）：
$$Odds(A)=\frac{P(A)}{1-P(A)}=\frac{事件A发生的概率}{事件A不发生的概率}$$
$$Odds(A) \subset[0,+\infty)$$

几率（Odds） 反应一个事件发生是该事件发生和不发生的比率
后验概率Posterior probability P(y|x)
后验概率P(y|x)属于条件概率的一种，指的是在给定证据X后，参数y的概率。

$$P(y|x) \subset[0,1]$$

在神经网络模型中，通常将经过激活函数的(0,1)范围的输出层值作为作为**后验概率P(y|x)**

$$P(y|x)=sigmod(Wx+b)$$

似然性（likelihood）
“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性”或“概率”又有明确的区分。

概率(probability) 用于在已知一些参数$x$的情况下，预测接下来的观测所得到的结果y; $P(y|x)$

似然性(likelihood) 则是用于在已知某些观测所得到的结果y时，对有关事物的性质的参数x进行估计。$L(x|y)$
参数估计
最大似然估计（MLE）

已知一组数据集D是独立地从概率分布P上采样生成的，且 [公式] 具有确定的形式（如高斯分布，二项分布等）但参数 [公式] 未知。

问题：如何根据数据集[公式] 估计参数[公式] ?

为了解决上述问题，统计学界存在两种不同的解决方案：

频率学派：参数[公式] 是一个客观存在的固定值，其可以通过找到使数据集 [公式] 出现可能性最大的值，对参数 [公式] 进行估计，此便是极大似然估计的核心思想。
贝叶斯学派：参数 [公式] 是一个随机变量，服从一个概率分布（换句话讲， [公式] 不是一个客观存在的固定值，而是可以取很多不同值的变量，且具有相应的可能性），其首先根据主观的经验假定[公式]的概率分布为 [公式] （先验分布，往往并不准确），然后根据观察到的新信息（数据集 [公式] ）对其进行修正，此时[公式]的概率分布为 [公式] （后验分布）。
最大似然估计
核心思想：找到使数据集 [公式] 出现可能性最大的值，对参数 [公式] 进行估计，即[公式]

最大后验估计
原则上，贝叶斯学派对 [公式] 的估计应该就是[公式]的后验分布[公式]，但是大多数时候后验分布的计算较为棘手，因此此时出现一种折衷解法：找到使后验概率最大的值，对参数 [公式] 进行估计，即

[公式]

[公式] （大名鼎鼎的贝叶斯公式）

[公式] （ [公式] 与 [公式] 无关）

[公式] （取 [公式] 不影响最优值）

根据上式可以发现，最大后验估计与最大似然估计优化过程中的差异便是多了一项 [公式] ，相当于加了一项与 [公式] 的先验概率 [公式] 有关的惩罚项。
在参数估计中有一类方法叫做“最大似然估计”,因为涉及到的估计函数往往是是指数型族,取对数后不影响它的单调性但会让计算过程变得简单,所以就采用了似然函数的对数,称“对数似然函数”。
根据涉及的模型不同,对数函数会不尽相同,但是原理是一样的,都是从因变量的密度函数的到来,并涉及到对随机干扰项分布的假设

给定输出y时，关于参数的x似然函数$L(x|y)$（在数值上）等于给定参数x后变量y的概率$P(y|x)$：
$$ L(x|y) = P(y|x)$$

Logit变换与对数机率函数
Logit变换 是指log it(它)，Logit Odds 就是对Odds 进行log(Odds)计算

对上式进行Logit变换,形如下面的则称为正样本的对数机率 z
$$z=ln(Odds(A))=ln\frac{P(A)}{1-P(A)}$$
$$z \subset(-\infty,+\infty)$$

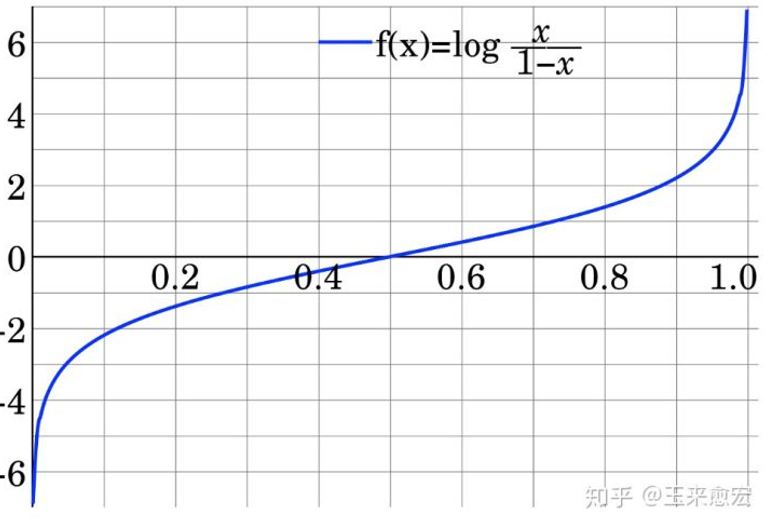
数学上
$$ln\frac{P(A)}{1-P(A)}=z$$
可以推出，概率P(A) 形式如下：
$$P(A)=f(z)=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^{z}} $$

$f(z)=\frac{1}{1+e^{-z}}$称为对数机率函数 ，其数形式与Sigmoid 函数相同

2.2.2. 函数的讨论

log对数函数（logarithmic loss function)，又称为 对数似然函数(log-likehood loss function) ，是对单个样本的描述，表示为
$$Loss(y,P(y|x))$$

是关于实际值y，与特征值x下的后验概率P(y|x) 的函数，log对数等于后验概率的对数。这个函数的值通过下面的log函数的标准形式计算：

$$Loss(y,P(y|x))=-\log{P(y|x)}$$

$$Coss(y,P(y|x))=-\frac{1}{N} \sum{log{P(y|x)}}$$

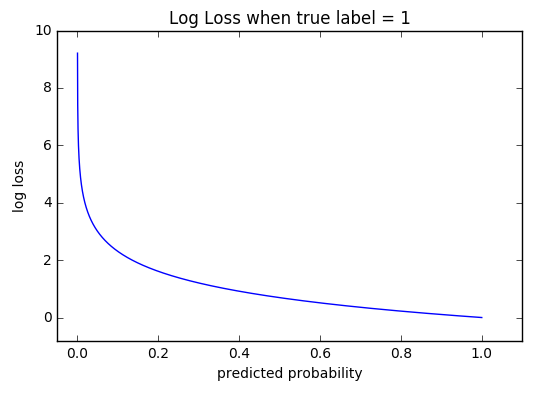
2.2.3. 对于二分类问题

二分类问题的后验概率P(label=0|x)（当输入为x时，label=0的概率）,可知

$$P(label=0|x)=1-P(label=1|x)$$

$$P(label=0|x) \subset[0,1]$$

机率Odds(label=0|x)”

$$Odds(label=0|x) =\frac{P(label=0|x)}{1-P(label=0|x)}\subset[0,+\infty)$$
若令$y=P(label=0|x)$,则正样本（label=0）的对数机率 z

$$ln\frac{y}{1-y}=ln\frac{P(label=0|x)}{P(label=1|x)}=z$$

$$z\subset(-\infty,+\infty)$$

依据输入特征x，确定该特征对应的label=0的概率为$P(label=0|x)$

$$P(label=0|x)=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^{z}}$$

依据输入特征x，确定该特征对应的label=1的概率为$P(label=1|x)$，
$$P(label=1|x)=1-P(label=0|x)=\frac{1}{1+e^{z}}$$

若 z=wx+b 即
$$P(label∣x)=\begin{cases}
\frac{e^z}{1+e^{z}}=\frac{e^{wx+b}}{1+e^{wx+b}}, label=0\
\frac{1}{1+e^{z}}=\frac{1}{1+e^{wx+b}}, label=1\
\end{cases}
$$

$$Loss(y,P(y|x))=-\log {P(y|x)}=\begin{cases}
-\log{\frac{e^z}{1+e^{z}}}, y=0\
-\log{\frac{1}{1+e^{z}}}, y=1\
\end{cases}
$$

$$Coss(y,P(y|x))=\frac{1}{n}\sum{Loss(y,P(y|x))}$$

$$Coss(y,P(y|x))=\frac{1}{n_0+n_1}(\sum_{i=1}^{n_0}{Loss(y=0,P(y=0|x))}+\sum_{i=1}^{n_}{Loss(y=1,P(y=1|x))}) $$ $$Coss(y,P(y|x))=\frac{1}{n_0+n_1}(\sum_{i=1}^{n_0}{-1*log(P(1|x))}+\sum_{i=1}^{n_}{(1-0)log(1-p(1|x))})$$

手动：

import numpy as np

# y_true ==labels
# y_pred ==predictions

def logcoss(y_true, y_pred, eps=1e-15):
    # Prepare numpy array data
    y_true = np.array(y_true)
    y_pred = np.array(y_pred) 
    assert (len(y_true) and len(y_true) == len(y_pred))
    # Clip y_pred between eps and 1-eps
    p = np.clip(y_pred, eps, 1-eps)
    loss = np.sum(- y_true * np.log(p) - (1 - y_true) * np.log(1-p))
    cost=loss / len(y_true)
    return cost

封装：

$$logloss=weights\times(labels\times \log{(predictions+epsilon)} + (1-labels)* \log{(1-predictions+epsilon)}) $$

$$logloss=W\times(L\times\log{(P+e)} + (1-L)\times\log{(1-P+e)}) $$

log_loss=tf.losses.log_loss(
    labels,
    predictions, 
    weights=1.0,
    epsilon=1e-07, 
    scope=None,
    loss_collection=tf.GraphKeys.LOSSES,
    reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)
# 注意
If reduction is NONE, this has the same shape as labels; otherwise, it is scalar.


log_loss=tf.losses.log_loss(y_true,y_predict,reduction=None)
type(log_loss)
>>> Tensor 
log_loss_results=sess.run(log_loss)
# log_loss_results.shape =y_true.shape 
log_cost=tf.reduce_sum(log_loss)


log_loss=tf.losses.log_loss(y_true,y_predict)
type(log_loss)
>>> Tensor 
log_loss_results=sess.run(log_loss)
# log_loss_results 标量

type(log_cost)
>>> 标量

2.2.4. 对于多分类问题

应用
Logistic回归

2.3. Hinge损失函数

$$loss(y_,y)=max(0,1-y_ · y)$$

手动：

loss = tf.maximum(0.0, 1.0-tf.multiply(real_label, predict_label))
# loss shape =real_label.shape==predict_label.shape
cost = tf.reduce_mean(loss,axis=None,keep_dims=False,name=None,reduction_indices=None)
# cost shape= ()  is a  val 数字

封装：

hinge_loss=tf.losses.hinge_loss(
    labels,
    logits,
    weights=1.0,
    scope=None,
    loss_collection=tf.GraphKeys.LOSSES,
    reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)

应用
Hinge loss用于最大间隔（maximum-margin）分类，其中最有代表性的就是支持向量机SVM。

3. 回归损失

3.1. 绝对值损失函数

$$Loss(y_ ,y)=|y_ -y|$$

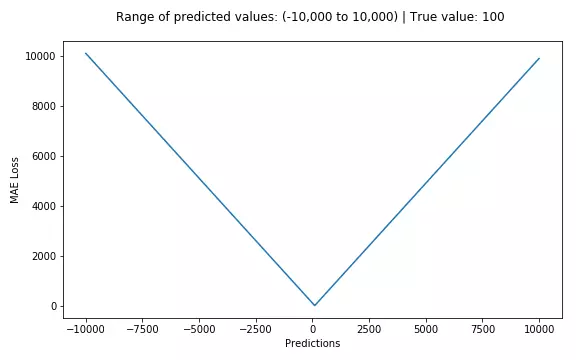
手动：

# real_label shape =(N,···)
# predict_label shape =(N,···)
# predict_label.shape==real_label.shape
loss=tf.abs(tf.subtract(real_label, predict_label))
# loss shape =(N,···)
cost = tf.reduce_mean(loss,axis=None,keep_dims=False,name=None,reduction_indices=None)
# cost shape= ()  is a  val 数字

封装：

loss=tf.losses.absolute_difference(
    labels,
    predictions,
    weights=1.0,
    scope=None,
    loss_collection=tf.GraphKeys.LOSSES,
    reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)

3.2. 平方损失函数

$$loss(y_,y)=\frac{1}{N}\sum_{i=1}^{N}{(y_-y)^2}$$

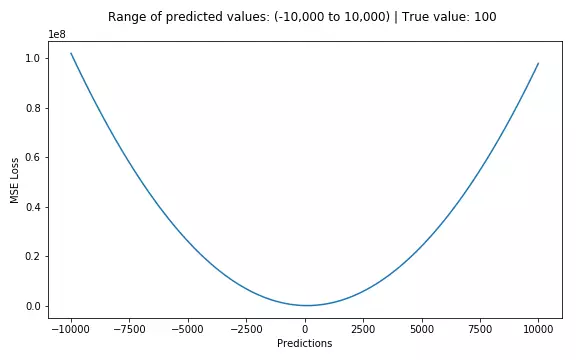
手动：

# real_label shape =(N,···)
# predict_label shape =(N,···)
# predict_label.shape==real_label.shape
loss=tf.abs(tf.subtract(real_label, predict_label))
# loss shape =(N,···)
cost = tf.reduce_mean(loss,axis=None,keep_dims=False,name=None,reduction_indices=None)
# cost shape= ()  is a  val 数字

封装：

mean_squared_error=tf.losses.mean_squared_error(
    labels,
    predictions,
    weights=1.0,
    scope=None,
    loss_collection=tf.GraphKeys.LOSSES,
    reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)
# mean_squared_error shape =() is a value

# 平方函数实际为 均方差（MSE）
mean_squared_error,update_op=tf.metrics.mean_squared_error(
    labels,
    predictions, #　predictions　为predict＿label
    weights=None,
    metrics_collections=None,
    updates_collections=None,
    name=None
)
# mean_squared_error shape =() is a value

示例

import tensorflow as tf
a = tf.constant([[4.0, 4.0, 4.0], [3.0, 3.0, 3.0], [1.0, 1.0, 1.0]])
b = tf.constant([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0], [2.0, 2.0, 2.0]])

cost = tf.losses.mean_squared_error(a, b)     
mse_op, mse_update_op= tf.metrics.mean_squared_error(a, b, name="mse")
init_op=tf.initialize_all_variables()
init_op2=tf.initialize_local_variables()
sess.run(init_op2)
sess.run(init_op)

sess.run(cost) #4.6666665
sess.run(mse_update_op) #4.6666665

应用：
最小二乘法通常用欧式距离进行距离的度量,使用平方损失函数

3.3. 指数损失函数

$$loss(y_,y)=e^{-y_·y}=\frac{e^y} {e^{y_}}$$

$$coss(y_,y)=\frac{1}{N}\sum_{i=1}^{N}{e^{-y_·y}}$$

Tensorflow中没有指数损失函数的封装包，可以自定义

# real_label.shape ==predict_label.shape==(counts,····)
loss=tf.exp(tf.multiply(-real_label,predict_label))
# loss shape =(counts,····)
cost = tf.reduce_mean(loss,axis=None,keep_dims=False,name=None,reduction_indices=None)
# cost shape= ()  is a  val 数字

应用
AdaBoost使用指数损失函数。

关于Adaboost的推导，可以参考Wikipedia：AdaBoost或者《统计学习方法》P145.

3.4. Huber损失函数

Huber损失函数，平滑平均绝对误差相比平方误差损失，Huber损失对于数据中异常值的敏感性要差一些。在值为0时，它也是可微分的。它基本上是绝对值，在误差很小时会变为平方值。误差使其平方值的大小如何取决于一个超参数δ，该参数可以调整。当δ~ 0时，Huber损失会趋向于MAE；当δ~ ∞（很大的数字），Huber损失会趋向于MSE。

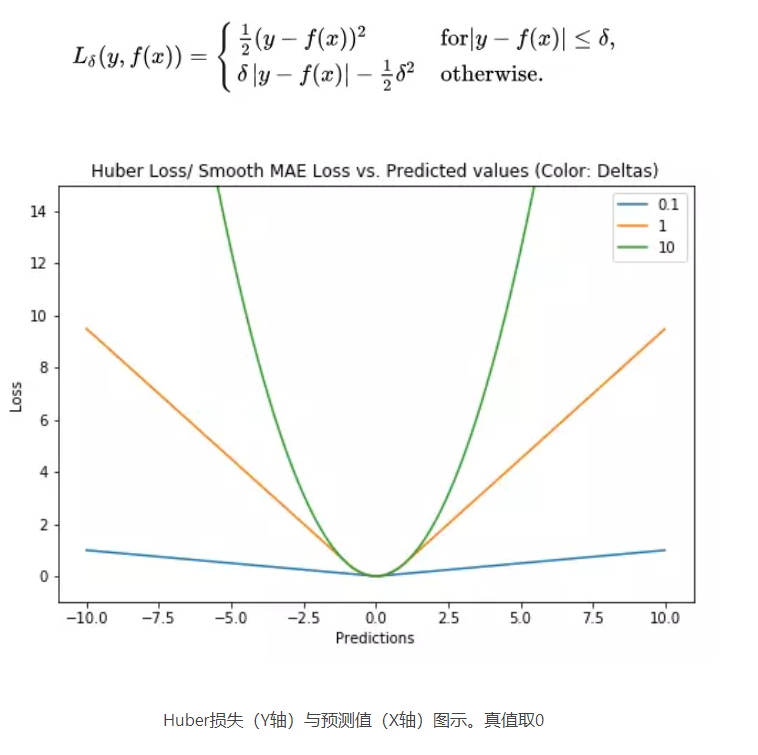
使用MAE训练神经网络最大的一个问题就是不变的大梯度，这可能导致在使用梯度下降快要结束时，错过了最小点。而对于MSE，梯度会随着损失的减小而减小，使结果更加精确。

在这种情况下，Huber损失就非常有用。它会由于梯度的减小而落在最小值附近。比起MSE，它对异常点更加鲁棒。因此，Huber损失结合了MSE和MAE的优点。但是，Huber损失的问题是我们可能需要不断调整超参数delta。

# huber 损失
def huber(true, pred, delta):
    loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
    return np.sum(loss)

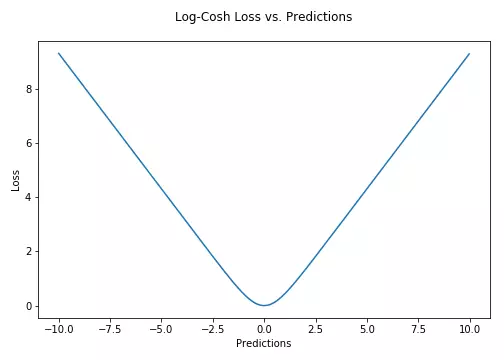
3.5. Log-Cosh损失

Log-cosh是另一种应用于回归问题中的，且比L2更平滑的的损失函数。它的计算方式是预测误差的双曲余弦的对数。
$$Loss=\sum_{i}^{n}{\log{cosh(\hat{y}-y)}}$$

优点：
1. 不易受到异常点的影响。对于较小的x，log(cosh(x))近似等于(x^2)/2，对于较大的x，近似等于abs(x)-log(2)。这意味着‘logcosh’基本类似于均方误差，但不易受到异常点的影响。
2. 二阶处处可微。它具有Huber损失所有的优点，但不同于Huber损失的是，Log-cosh二阶处处可微。

为什么需要二阶导数？许多机器学习模型如XGBoost，就是采用牛顿法来寻找最优点。而牛顿法就需要求解二阶导数（Hessian）。因此对于诸如XGBoost这类机器学习框架，损失函数的二阶可微是很有必要的。

XgBoost中使用的目标函数。注意对一阶和二阶导数的依赖性

但Log-cosh损失也并非完美，其仍存在某些问题。比如误差很大的话，一阶梯度和Hessian会变成定值，这就导致XGBoost出现缺少分裂点的情况。

4. 熵

4.1. 熵--当只有一个变量分布

熵是对于给定分布 $q(x)$ 的不确定性的度量，当取自有限的样本时，熵的公式可以表示为。

$$H(q(x))=-\sum{q(x) \log{q(x)} }$$

如果我们已知所有的点都是绿色的，单一的？那个分布的不确定性是0，熵为0。
如果我们已知，数据点服从q（x）分布，我们可以依据上式计算该分布的熵

4.2. 交叉熵--当有2个变量分布

在信息论中，基于相同事件测度的两个概率分布 P(x)和 q(x)的交叉熵是指，
$$H(P(x),q(x))=-\sum{P(x) \log{q(x)} }$$

交叉熵是用来描述p分布和q分布的距离

4.3. 实际应用

现实情况中，多数情况式我们不知道数据的的真实分布。假设，数据真实分布为q(y)，我们推测其分为P（y_）。如果我们像这样计算熵，我们实际上是在计算两个分布之间的交叉熵：

$$H(q(y),P(y_))=-\sum{q(y) * \log{ P(y_ ) } }$$

模型训练的目的就是使预测分布P(x) 逼近 q(x)，他们之间距离越小，函数越小。

learning to rank 算法

learning to rank 算法归纳为：
1. PointWise，
2. PairWise，
3. ListWise

Pointwise和Pairwise把排序问题转换成回归、分类或有序分类问题。Lisewise把Query下整个搜索结果作为一个训练的实例。3种方法的区别主要体现在损失函数（Loss Function）上。

PointWise

PairWise

$$L(F(x),y)=∑{i=1}^{n−1}∑^n l(sign(y_i−y_j),f(x_i)−f(x_j))$$

另外，有的Pairwise方法没有考虑到排序结果前几名对整个排序的重要性，也没有考虑不同查询对应的文档集合的大小对查询结果的影响(但是有的Pairwise方法对这些进行了改进，比如IR SVM就是对Ranking SVM针对以上缺点进行改进得到的算法)。

5. 参考资料

机器学习大牛最常用的5个回归损失函数，你知道几个？:https://www.jiqizhixin.com/articles/2018-06-21-3 ↩